
分析 本题应分两种情况进行讨论:
(1)当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的周长求出;
(2)当△ABC为钝角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△ABC的周长求出.
解答 解:此题应分两种情况说明: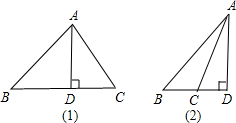
(1)当△ABC为锐角三角形时,
在Rt△ABD中,BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{2{0}^{2}-1{2}^{2}}$=16,
在RT△ADC中,CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
即可得BC=BD+CD=21,故可得△ABC的周长=AB+BC+CA=54;
(2)当△ABC为钝角三角形时,
在Rt△ABD中,BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{2{0}^{2}-1{2}^{2}}$=16,
在RT△ADC中,CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
即可得BC=BD-CD=11,故可得△ABC的周长=AB+BC+CA=44.
故△ABC的周长为54或44.
点评 此题考查了勾股定理及解直角三角形的知识,在解本题时应分两种情况进行讨论,易错点在于漏解,同学们思考问题一定要全面,有一定难度.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图的正方形网格,每个正方形边长为1.
如图的正方形网格,每个正方形边长为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
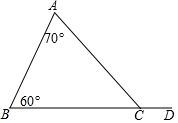 如图,△ABC中,∠A=70°,∠B=60°,∠ACD是△ABC的一个外角,能由∠A,∠B求出∠ACD吗?如果能,∠ACD与∠A,∠B有什么关系?
如图,△ABC中,∠A=70°,∠B=60°,∠ACD是△ABC的一个外角,能由∠A,∠B求出∠ACD吗?如果能,∠ACD与∠A,∠B有什么关系?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
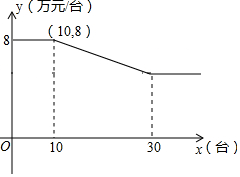 某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系如图所示.
某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com