
【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.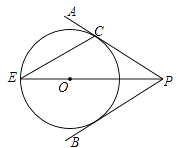
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.
【答案】
(1)证明:连接OC,作OD⊥PB于D点.
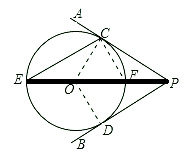
∵⊙O与PA相切于点C, ∴OC⊥PA
(2)解:设PO交⊙O于F,连接CF.
∵OC=3,PC=4,∴PO=5,PE=8.
∵⊙O与PA相切于点C, ∴∠PCF=∠E.
又∵∠CPF=∠EPC, ∴△PCF∽△PEC,
∴CF:CE=PC:PE=4:8=1:2.
∵EF是直径, ∴∠ECF=90°.
设CF=x,则EC=2x.
则x2+(2x)2=62, 解得x= ![]() .
.
则EC=2x= ![]() .
.
【解析】要证明直线PB与⊙O相切,添加辅助线连接OC,作OD⊥PB于D点,再证明OD是圆的半径,根据角平分线上的点到角两边的距离相等及切线的性质,易证得结论。
(2)根据已知易证得△PCF∽△PEC,得出对应边成比例,证出CF:CE=1:2.再根据EF是直径得出△CEF是直角三角形,利用勾股定理求解即可。


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,点![]() 为坐标原点,
为坐标原点,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() 且
且![]() ,其中
,其中![]() ,
,![]() 满足
满足![]() .
.



(1)求点![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 轴负方向运动,设点
轴负方向运动,设点![]() 的运动时间为
的运动时间为![]() 秒.连接
秒.连接![]() 、
、![]() ,用含有
,用含有![]() 的式子表示
的式子表示![]() 的面积为
的面积为![]() (直接写出
(直接写出![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,是否存在![]() 的值,使得
的值,使得![]() ,若存在,请求出
,若存在,请求出![]() 的值,并直接写出
的值,并直接写出![]() 中点
中点![]() 的坐标;若不存,请说明理由.
的坐标;若不存,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球,8个黑球,7个红球.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个球是黑球的概率是 ![]() ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,AB⊥AC,点E是BC的中点,AE与BD交于点F,且F是AE的中点.
(Ⅰ)求证:四边形AECD是菱形;(Ⅱ)若AC=4,AB=5,求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电商场计划用9万元从生产厂家购进50台电视机,已知该厂家生产3种不同型号的电视机,出厂价分别为A种每台1500元,B种每台2100元,C种每台2500元.
(1)若家电商场同时购进两种不同型号的电视机共50台,用去9万元,请你计算一下商场有哪几种进货方案?
(2)若商场销售一台A种电视机可获利150元,销售一台B种电视机可获利200元,销售一台C种电视机可获利250元,在同时购进两种不同型号的电视机方案中,为了使销售时获利最多,应选择哪种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设直线y=kx+6和直线y=(k+1)x+6(k是正整数)及x轴围成的三角形面积为Sk(k=1,2,3,…,8),则S1+S2+S3+…+S8的值是( )
A. ![]() B.
B. ![]() C. 16D. 14
C. 16D. 14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC在x轴正半轴上,点A在第一象限,延长AB交y轴负半轴于点D,延长CA到点E,使AE=AC,双曲线y= ![]() (x>0)的图象过点E.若△BCD的面积为2
(x>0)的图象过点E.若△BCD的面积为2 ![]() ,则k的值为( )
,则k的值为( )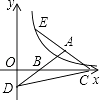
A.4 ![]()
B.4
C.2 ![]()
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com