
 某直升飞机在我方追击炮阵地M上方测得敌军雷达站P的俯角为15°,在向点P的迎面沿仰角30°的方向飞行,升高100米后再测点P的俯角为30°,分别求原飞行高度和点M到点P的水平距离(tan15°=2-$\sqrt{3}$,cot15°=2+$\sqrt{3}$)
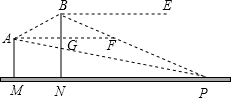
某直升飞机在我方追击炮阵地M上方测得敌军雷达站P的俯角为15°,在向点P的迎面沿仰角30°的方向飞行,升高100米后再测点P的俯角为30°,分别求原飞行高度和点M到点P的水平距离(tan15°=2-$\sqrt{3}$,cot15°=2+$\sqrt{3}$) 分析 作PQ⊥AF,由题意知∠1=15°,∠2=∠3=∠4=30°,BG=100米,先求出AG=GF=100$\sqrt{3}$,设PQ=x,知FQ=$\sqrt{3}$x,根据tan∠1=$\frac{PQ}{AQ}$求出x的值即可得.
解答 解:如图,作PQ⊥AF交AF延长线于点Q,
由题意知∠1=15°,∠2=∠3=∠4=30°,BG=100米,
在Rt△ABG中,AG=$\frac{BG}{tan∠2}$=$\frac{100}{\frac{\sqrt{3}}{3}}$=100$\sqrt{3}$,
在Rt△BGF中,GF=BGtna∠GBF=100tan60°=100$\sqrt{3}$,
∴AF=AG+GF=200$\sqrt{3}$,
设PQ=x,则FQ=$\frac{PQ}{tan∠4}$=$\frac{x}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$x,
∴AQ=AF+FQ=200$\sqrt{3}$+$\sqrt{3}$x,
由tan∠1=$\frac{PQ}{AQ}$可得$\frac{x}{200\sqrt{3}+\sqrt{3}x}$=2-$\sqrt{3}$,
解得:x=100$\sqrt{3}$,
即PQ=AM=100$\sqrt{3}$,
则MP=AQ=200$\sqrt{3}$+$\sqrt{3}$×100$\sqrt{3}$=300+200$\sqrt{3}$,
答:原飞行高度为100$\sqrt{3}$米,点M到点P的水平距离为(300+200$\sqrt{3}$)米.
点评 本题主要考查解直角三角形的仰角与俯角的应用,根据已知构造直角三角形利用锐角三角函数关系得出是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+a=a2 | B. | a2•2a3=2a6 | C. | $\sqrt{6a}$÷$\sqrt{2a}$=3 | D. | (-ab3)2=a2b6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
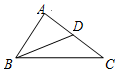 如图,在△ABC中,点D是边AC的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示).
如图,在△ABC中,点D是边AC的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com