
【题目】如图,一艘海轮位于灯塔P的南偏东30°方向,距离灯塔100海里的A处,它计划沿正北方向航行,去往位于灯塔P的北偏东45°方向上的B处.

(1)问B处距离灯塔P有多远?(结果精确到0.1海里)
(2)假设有一圆形暗礁区域,它的圆心位于射线PB上,距离灯塔150海里的点O处.圆形暗礁区域的半径为60海里,进入这个区域,就有触礁的危险.请判断海轮到达B处是否有触礁的危险?如果海轮从B处继续向正北方向航行,是否有触礁的危险?并说明理由.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
【答案】(1)70.7海里;(2)有触礁的危险,理由见解析
【解析】
(1)作PD⊥AB于点D,由PA=100,∠APD=60°,∠BPD=45°知∠A=30°,从而得PD=50,再由BD=PD=50知PB=50![]() ≈70.7.
≈70.7.
(2)过点O作OE⊥AB,交AB延长线于点E,由OE≈56.07<60即可判断.
(1)过点P作PD⊥AB于点D.

依题意可知,PA=100,∠APD=60°,∠BPD=45°.
∴∠A=30°.
∴PD=50.
在△PBD中,BD=PD=50,
∴PB=50![]() ≈70.7.
≈70.7.
答:B处距离灯塔P约70.7海里.
(2)依题意知:OP=150,OB=150﹣50![]() .
.
∴海轮到达B处没有触礁的危险.
过点O作OE⊥AB,交AB延长线于点E,
∵∠OBE=∠PBD=45°,
∴OE=OBsin∠OBE=(150﹣50![]() )×
)×![]() =75
=75![]() ﹣50≈56.07<60,
﹣50≈56.07<60,
∴海轮从B处继续向正北方向航行,有触礁的危险.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


查看答案和解析>>
科目:初中数学 来源: 题型:
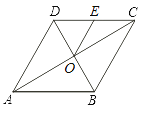
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )
A. ![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角△ABC中,AB=AC,边BC长为6,高AD长为4,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,则正方形PQMN的边长为( )
A.![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E、F分别是边AD、AB上的点,连结OE、OF、EF.若AB=7,BC=5![]() ,∠DAB=45°,则①点C到直线AB的距离是_____.②△OEF周长的最小值是________.
,∠DAB=45°,则①点C到直线AB的距离是_____.②△OEF周长的最小值是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
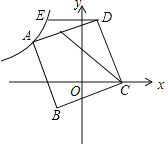
【题目】如图,在平面直角坐标系中,正方形ABCD顶点B(﹣1,﹣1),C在x轴正半轴上,A在第二象限双曲线y=﹣![]() 上,过D作DE∥x轴交双曲线于E,连接CE,则△CDE的面积为( )
上,过D作DE∥x轴交双曲线于E,连接CE,则△CDE的面积为( )
A.3B.![]() C.4D.
C.4D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() (x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD//y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
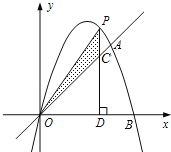
【题目】如图,已知抛物线y=ax2+bx+c的图象经过点A(3,3)、B(4,0)和原点O,P为直线OA上方抛物线上的一个动点.
(1)求直线OA及抛物线的解析式;
(2)过点P作x轴的垂线,垂足为D,并与直线OA交于点C,当△PCO为等腰三角形时,求D的坐标;
(3)设P关于对称轴的点为Q,抛物线的顶点为M,探索是否存在一点P,使得△PQM的面积为![]() ,如果存在,求出P的坐标;如果不存在,请说明理由.
,如果存在,求出P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】植树节期间,某校倡议学生利用双休日“植树”劳动,为了解同学们劳动情况.学校随机调查了部分学生的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回顾下列:
(1)通过计算,将条形图补充完整;
(2)扇形图形中“1.5小时”部分圆心角是 ;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com