
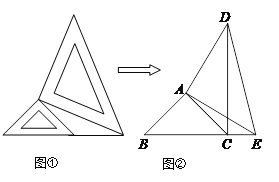
【题目】两个大小不同的等腰直角三角板如图①所示放置,图②是由它抽象出来的几何图形,点B、C、E在同一条直线上,连结DC.
(1)请找出图②中的全等三角形,并给予证明;
(2)求证:DC⊥BE.
【答案】(1)△ACD≌△ABE(2)证明见解析
【解析】试题分析:(1)根据等腰直角三角形的性质可以得出AB=AC,AE=AD,∠BAC=∠EAD,进而得到∠BAE=∠CAD,即可得到结论;
(2)由△ABE≌△ACD可以得出∠ACD=∠ABE,进而得出∠BCD =90°,由此可以得出结论.
试题解析:(1)解:△ACD≌△ABE. 证明如下:
∵△ABC与△AED均为等腰直角三角形,∴AB=AC,AE=AD,∠BAC=∠EAD=90°,∴∠BAC+∠CAE=∠EAD+∠CAE,即∠BAE=∠CAD.
在△ABE与△ACD中,∵AB=AC,∠BAE=∠CAD,AE=AD,∴△ABE≌△ACD(SAS).
(2)证明:∵△ABC是等腰直角三角形,∴∠ABC=∠ACB=45°.
由(1)可知△ABE≌△ACD,∴∠ACD=∠ABE=45°,∴∠BCD=∠ACB+∠ACD=90°,∴DC⊥BE.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,边长为2的正五边形ABCDE内接于⊙O,AB、DC的延长线交于点F,过点E作EG∥CB交BA的延长线于点G.

(1)求证: ![]() ;
;
(2)证明:EG与⊙O相切,并求AG、BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
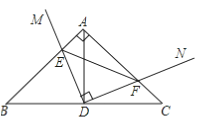
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D为BC的中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,下列结论:①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF,其中正确结论是( )
A. ①②④ B. ②③④
C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下四种沿![]() 折叠的方法中,不一定能判定纸带两条边线
折叠的方法中,不一定能判定纸带两条边线![]() ,
, ![]() 互相平行的是( ).
互相平行的是( ).

A. 如图![]() ,展开后测得
,展开后测得![]()
B. 如图![]() ,展开后测得
,展开后测得![]()
C. 如图![]() ,测得
,测得![]()
D. 如图![]() ,展开后再沿
,展开后再沿![]() 折叠,两条折痕的交点为
折叠,两条折痕的交点为![]() ,测得
,测得![]() ,
, ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
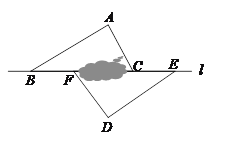
【题目】如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l外有不重合的两点A、B.在直线l上求一点C,使得![]() 的长度最短,作法为:①作点B关于直线l的对称点B'.②连接AB'交直线l于点C,则点C即为所求.在解决这个问题时,没有用到的知识点是( )
的长度最短,作法为:①作点B关于直线l的对称点B'.②连接AB'交直线l于点C,则点C即为所求.在解决这个问题时,没有用到的知识点是( )

A. 线段的垂直平分线性质 B. 两点之间线段最短
C. 三角形两边之和大于第三边 D. 角平分线的性质
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生的艺术特长发展情况,某校音乐组决定围绕“在舞蹈、乐器、声乐、戏曲、其它活动项目中,你最喜欢哪一项活动(每人只限一项)”的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制成如下两幅不完整的统计图.

请你根据统计图解答下列问题:
(1)在这次调查中一共抽查了____名学生,其中,喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为____,喜欢“戏曲”活动项目的人数是____人;
(2)若在“舞蹈、乐器、声乐、戏曲”活动项目任选两项设立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,若∠A=50°,∠B=55°,则△ABC是____________三角形;若∠A=50°,∠B=25°,则△ABC是____________三角形.(填“锐角”,“直角”或“钝角”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com