
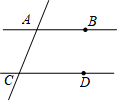
 如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α-β,③β-α,④360°-α-β,∠AEC的度数可能是( )
如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α-β,③β-α,④360°-α-β,∠AEC的度数可能是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
分析 根据点E有4种可能位置,分四种情况进行讨论,分别画出图形,依据平行线的性质以及三角形外角性质进行计算求解即可.
解答 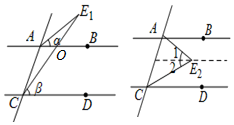 解:点E有4种可能位置.
解:点E有4种可能位置.
(1)如图,由AB∥CD,可得∠AOC=∠DCE1=β,
∵∠AOC=∠BAE1+∠AE1C,
∴∠AE1C=β-α.
(2)如图,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,
∴∠AE2C=α+β.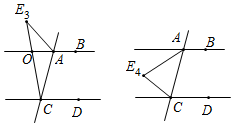
(3)如图,由AB∥CD,可得∠BOE3=∠DCE3=β,
∵∠BAE3=∠BOE3+∠AE3C,
∴∠AE3C=α-β.
(4)如图,由AB∥CD,可得∠BAE4+∠AE4C+∠DCE4=360°,
∴∠AE4C=360°-α-β.
∴∠AEC的度数可能为β-α,α+β,α-β,360°-α-β.
故选:D.
点评 本题主要考查了平行线的性质的运用,解题时注意:两直线平行,同位角相等,两直线平行,内错角相等.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
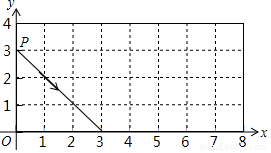 如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2017次碰到矩形的边时,此时点P的坐标为( )
如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2017次碰到矩形的边时,此时点P的坐标为( )| A. | (0,3) | B. | (3,0) | C. | (1,4) | D. | (7,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
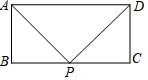 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a,b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a,b间的关系式一定满足( )| A. | ${a^2}≥\frac{1}{4}{b^2}$ | B. | a2≥b2 | C. | ${a^2}≥\frac{9}{4}{b^2}$ | D. | a2≥4b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 鞋店老板比较关心的是一周内卖出的鞋的尺码组成的一组数据的众数 | |
| B. | 某种彩票的中奖率是2%,则买50张这种彩票一定会中奖 | |
| C. | “打开电视,正在播放《新闻联播》”是必然事件 | |
| D. | 若甲组数据方差S甲2=0.06,乙组数据的方差S乙2=0.1,则乙组数据比甲组数据稳定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com