
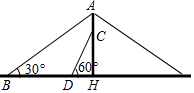
 芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,在同类型重载桥梁中,它的主跨度居世界第二.如图,是该桥面上的一根立柱和拉索的示意图,小明测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索底端距离BD为20米,且已知两拉索顶端的距离AC为2米,请求出立柱AH的长.(结果精确到0.1米,$\sqrt{3}$≈1.732)
芜湖长江大桥是中国跨度最大的公路和铁路两用桥梁,在同类型重载桥梁中,它的主跨度居世界第二.如图,是该桥面上的一根立柱和拉索的示意图,小明测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索底端距离BD为20米,且已知两拉索顶端的距离AC为2米,请求出立柱AH的长.(结果精确到0.1米,$\sqrt{3}$≈1.732) 分析 首先利用未知数表示出DH,CH,AH,BH的长,再利用BH=BD+DH得出等式求出答案.
解答 解:设DH=x,
∵∠CDH=60°,∠AHB=90°,
∴CH=DH•tan60°=$\sqrt{3}$x,
∴AH=AC+CH=2+$\sqrt{3}$x,
∵∠B=30°,
∴BH=$\sqrt{3}$AH=2$\sqrt{3}$+3x,
∵BH=BD+DH,
∴2$\sqrt{3}$+3x=20+x,
解得:x=10-$\sqrt{3}$,
∴AH=2+$\sqrt{3}$(10-$\sqrt{3}$)=10$\sqrt{3}$-1≈16.3(m),
答:立柱AH的长约为16.3m.
点评 此题主要考查了解直角三角形的应用,正确表示出BH的长是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
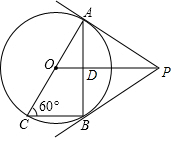 如图,已知AC是⊙O的直径,∠ACB=60°,连结AB,过A、B两点分别作⊙O的切线,两切线交于点P,连接OP交AB于D.
如图,已知AC是⊙O的直径,∠ACB=60°,连结AB,过A、B两点分别作⊙O的切线,两切线交于点P,连接OP交AB于D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
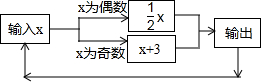 如图所示的运算程序中,若开始输入的x值为15,则第1次输出的结果为18,第2次输出的结果为9,…,第2017次输出的结果为( )
如图所示的运算程序中,若开始输入的x值为15,则第1次输出的结果为18,第2次输出的结果为9,…,第2017次输出的结果为( )| A. | 3 | B. | 4 | C. | 6 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
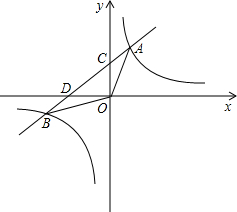 如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A、B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-3,0),A点的横坐标是3,tan∠CDO=$\frac{1}{3}$.
如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象相交于A、B两点,与y轴交于点C,与x轴交于点D,点D的坐标为(-3,0),A点的横坐标是3,tan∠CDO=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
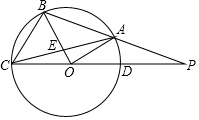 如图,A、B、C为⊙O上的点,PC过O点,交⊙O于D点,PD=OD,若OB⊥AC于E点.
如图,A、B、C为⊙O上的点,PC过O点,交⊙O于D点,PD=OD,若OB⊥AC于E点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
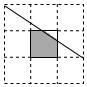 如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率为( )
如图,有16个格点,每个格点小正方形的面积为1,给图中间的小正方形内任意投点P,则点P落在图中阴影部分的概率为( )| A. | $\frac{5}{6}$ | B. | $\frac{7}{8}$ | C. | $\frac{9}{10}$ | D. | $\frac{11}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com