
P点为抛物线 (
( 为常数,
为常数, )上任一点,将抛物线绕顶点
)上任一点,将抛物线绕顶点 逆时针旋转
逆时针旋转 后得到的新图象与
后得到的新图象与 轴交于
轴交于 、
、 两点(点
两点(点 在点
在点 的上方),点
的上方),点 为点
为点 旋转后的对应点.
旋转后的对应点.
1.(1)当 ,点
,点 横坐标为4时,求
横坐标为4时,求 点的坐标;
点的坐标;
2.(2)设点 ,用含
,用含 、
、 的代数式表示
的代数式表示 ;
;
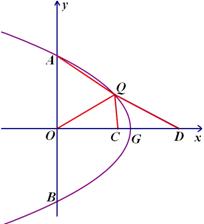
3.(3) 如图,点 在第一象限内, 点
在第一象限内, 点 在
在 轴的正半轴上,点
轴的正半轴上,点 为
为 的中点,
的中点, 平分
平分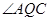 ,
, ,当
,当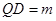 时,求
时,求 的值.
的值.
 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
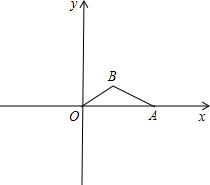 如图,在平面直角坐标系xOy中,△OAB的顶点A的坐标为(10,0),顶点B在第一象限内,且|AB|=3
如图,在平面直角坐标系xOy中,△OAB的顶点A的坐标为(10,0),顶点B在第一象限内,且|AB|=3| 5 |
| ||
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
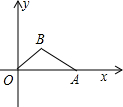 如图,在平面直角坐标系xOy中,△OAB的顶点A的坐标为(10,0),顶点B在第一象限内,且AB=3
如图,在平面直角坐标系xOy中,△OAB的顶点A的坐标为(10,0),顶点B在第一象限内,且AB=3| 5 |
| ||
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
P点为抛物线![]() (
(![]() 为常数,
为常数,![]() )上任一点,将抛物线绕顶点
)上任一点,将抛物线绕顶点![]() 逆时针旋转
逆时针旋转![]() 后得到的新图象与
后得到的新图象与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的上方),点
的上方),点![]() 为点
为点![]() 旋转后的对应点.
旋转后的对应点.

1.(1)当![]() ,点
,点![]() 横坐标为4时,求
横坐标为4时,求![]() 点的坐标;
点的坐标;
2.(2)设点![]() ,用含
,用含![]() 、
、![]() 的代数式表示
的代数式表示![]() ;
;
3.(3) 如图,点![]() 在第一象限内, 点
在第一象限内, 点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 为
为![]() 的中点,
的中点,![]() 平分
平分![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(36):2.7 最大面积是多少(解析版) 题型:解答题
 ,sin∠OAB=
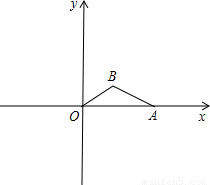
,sin∠OAB=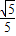 .
.
查看答案和解析>>
科目:初中数学 来源:第20章《二次函数和反比例函数》中考题集(36):20.5 二次函数的一些应用(解析版) 题型:解答题
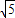 ,sin∠OAB=
,sin∠OAB= .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com