
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
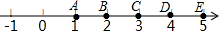 如图,在数轴上有A、B、C、D、E五个点表示相应的整数,无理数$\sqrt{13}$在两个点所表示的整数之间,这两个整数所对应的点是( )
如图,在数轴上有A、B、C、D、E五个点表示相应的整数,无理数$\sqrt{13}$在两个点所表示的整数之间,这两个整数所对应的点是( )| A. | 点A和点B | B. | 点B和点C | C. | 点C和点D | D. | 点D和点E |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
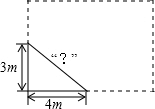 如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1米),却踩伤了花草.
如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1米),却踩伤了花草.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
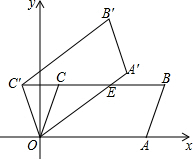 如图,在平面直角坐标系xOy中,平行四边形OABC的顶点A,B的坐标分别为(6,0),(7,3),将平行四边形OABC绕点O逆时针方向旋转得到平行四边形OA′B′C′,当点C′落在BC的延长线上时,线段OA′交BC于点E,则线段C′E的长度为5.
如图,在平面直角坐标系xOy中,平行四边形OABC的顶点A,B的坐标分别为(6,0),(7,3),将平行四边形OABC绕点O逆时针方向旋转得到平行四边形OA′B′C′,当点C′落在BC的延长线上时,线段OA′交BC于点E,则线段C′E的长度为5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
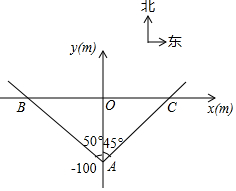 某段笔直的限速公路上,规定汽车的最高行驶速度不能超过60km/h(即$\frac{50}{3}$m/s),交通管理部门在离该公路100m处设置了一速度监测点A,在如图所示的坐标系中,A位于y轴上,测速路段BC在x轴上,点B在A的北偏西50°方向上,点C在点A的北偏东45°方向上.
某段笔直的限速公路上,规定汽车的最高行驶速度不能超过60km/h(即$\frac{50}{3}$m/s),交通管理部门在离该公路100m处设置了一速度监测点A,在如图所示的坐标系中,A位于y轴上,测速路段BC在x轴上,点B在A的北偏西50°方向上,点C在点A的北偏东45°方向上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
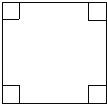 如图,面积为80cm2的大正方形的四个角是面积为5cm2的小正方形,现将这四个角剪掉,制作一个无盖的长方体盒子,求这个长方体的底面边长和高分别是多少?(结果保留根号)
如图,面积为80cm2的大正方形的四个角是面积为5cm2的小正方形,现将这四个角剪掉,制作一个无盖的长方体盒子,求这个长方体的底面边长和高分别是多少?(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com