
分析 根据分式的加法和除法可以化简题目中的式子,然后将a的值代入即可解答本题.
解答 解:($\frac{2}{a+1}$+$\frac{a+2}{{a}^{2}-1}$)÷$\frac{a}{a-1}$
=$\frac{2(a-1)+a+2}{(a+1)(a-1)}•\frac{a-1}{a}$
=$\frac{2a-2+a+2}{a(a+1)}$
=$\frac{3a}{a(a+1)}$
=$\frac{3}{a+1}$,
当a=2sin60°-tan45°=2×$\frac{\sqrt{3}}{2}$-1=$\sqrt{3}-1$时,原式=$\frac{3}{\sqrt{3}-1+1}=\frac{3}{\sqrt{3}}=\sqrt{3}$.
点评 本题考查分式的化简求值、特殊角的三角函数值,解答本题的关键是明确分式的化简求值的方法和知道特殊角的三角函数值.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:选择题
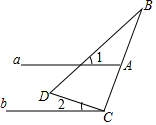 如图,直线a∥b,直角三角形如图放置,∠DCB=90°,若∠1+∠2=60°,则∠B的度数为( )
如图,直线a∥b,直角三角形如图放置,∠DCB=90°,若∠1+∠2=60°,则∠B的度数为( )| A. | 20° | B. | 40° | C. | 30° | D. | 25° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
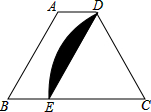 如图,四边形ABED是平行四边形,B、E、C三点共线,以点C为圆心,CDWie半径的弧与BC交于点E,AB=CD=4,则阴影部分的面积是$\frac{8}{3}$π-4$\sqrt{3}$.
如图,四边形ABED是平行四边形,B、E、C三点共线,以点C为圆心,CDWie半径的弧与BC交于点E,AB=CD=4,则阴影部分的面积是$\frac{8}{3}$π-4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com