
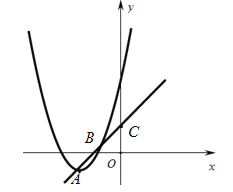
【题目】如图,二次函数与一次函数交于顶点![]() 和点
和点![]() 两点,一次函数与
两点,一次函数与![]() 轴交于点
轴交于点![]() .
.
(1)求二次函数![]() 和一次函数
和一次函数![]() 的解析式;
的解析式;
(2)![]() 轴上存在点
轴上存在点![]() 使
使![]() 的面积为9,求点
的面积为9,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)先把点![]() 代入抛物线的顶点式,用待定系数法求解析式,再由A、B坐标求出一次函数的解析式;
代入抛物线的顶点式,用待定系数法求解析式,再由A、B坐标求出一次函数的解析式;
(2)根据![]() 的面积=S△PCA-S△PBC=
的面积=S△PCA-S△PBC=![]() PC×(4-2)=9即可解答.
PC×(4-2)=9即可解答.
(1)解:设y1=a(x+4)2-1,把点![]() 代入解析式得,
代入解析式得,
3= a(-2+4)2-1,解得:a=1
∴![]() ;
;
设y2=kx+b,把![]() 和点
和点![]() 代入得
代入得
![]() 解得:
解得:![]()
所以,一次函数解析式为y=2x+7;
(2)∵![]() 、
、![]() ,点P在
,点P在![]() 轴上.
轴上.
∴点A、B到x轴的距离分别是4、2,
∴![]() 的面积=S△PCA-S△PBC=
的面积=S△PCA-S△PBC=![]() PC×(4-2)=9
PC×(4-2)=9
解得PC=9,
∵一次函数解析式为y=2x+7与x轴交于点C
∴C(0,7),OC=7,又∵PC=9
∴OP=7+9=16或OP=9-7=2
∴![]() 或P(0,16)
或P(0,16)


科目:初中数学 来源: 题型:
【题目】如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?

查看答案和解析>>
科目:初中数学 来源: 题型:
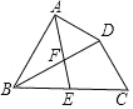
【题目】如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为____
查看答案和解析>>
科目:初中数学 来源: 题型:
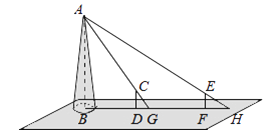
【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(2k+1)x+k2+1=0.
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两根恰好是一个矩形两邻边的长,且k=2,求该矩形的对角线L的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线C:y=x2+3x-10平移到C′.若两条抛物线C,C′关于直线x=1对称,则下列平移方法中正确的是( )
A. 将抛物线C向右平移![]() 个单位 B. 将抛物线C向右平移3个单位
个单位 B. 将抛物线C向右平移3个单位
C. 将抛物线C向右平移5个单位 D. 将抛物线C向右平移6个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com