
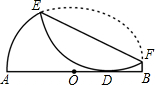
 已知半圆O的直径AB=4,沿它的一条弦折叠.
已知半圆O的直径AB=4,沿它的一条弦折叠.分析 (1)设折叠后的圆弧所在的圆心为O1,连接O1O,O1D,OE,设O1O交EF于点H,由折叠的轴对称性可知:EF垂直平分O1O,再证明OA=OB=OE=2,根据AD:DB=3:1,可知BD=1,OD=1,由勾股定理可知:O1O=$\sqrt{5}$,从而可知OH=$\frac{\sqrt{5}}{2}$,EH=$\frac{\sqrt{11}}{2}$,根据EF=2EH即可求得问题的答案;
(2)先根据题意画出图形,再求得最大值和最小值即可.
解答 解:(1)如图1-1,设折叠后的圆弧所在的圆心为O1,连接O1O,O1D,OE,设O1O交EF于点H.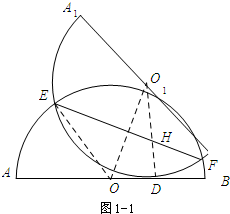
由折叠的轴对称性可知:EF是对称轴,
∴EF垂直平分O1O.
又∵EF是⊙O的弦,
∴010与EF相互垂直平分.
∵AB=4,
∴OA=OB=OE=2.
∵AD:DB=3:1,
∴BD=1,OD=1.
∴O1O═$\sqrt{O{D}^{2}+{O}_{1}{D}^{2}}=\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$.
∴OH=$\frac{\sqrt{5}}{2}$.
∴EH=$\sqrt{O{E}^{2}-O{H}^{2}}=\sqrt{{2}^{2}-(\frac{\sqrt{5}}{2})^{2}}$=$\frac{\sqrt{11}}{2}$.
∴EF=2EH=$\sqrt{11}$.
(2)如图1-2,折痕EF的有最小值,最小值=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$.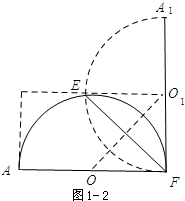
如图1-3,折痕EF的有最大值,最大值为2$\sqrt{3}$.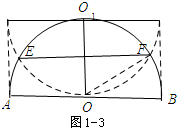
点评 本题主要考查的是切线的性质、折叠的性质、勾股定理的应用,利用切线的性质画出EF存在最大值和最小值时的图形时解题的关键.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:填空题
 甲、乙两工程队完成某项工程,甲先做了10天,然后乙加入合作,完成剩下的工程.设工程总量为1,若工程进度如下图所示,那么实际完成这项工程所用时间比甲单独完成此项工作所用时间少12天.
甲、乙两工程队完成某项工程,甲先做了10天,然后乙加入合作,完成剩下的工程.设工程总量为1,若工程进度如下图所示,那么实际完成这项工程所用时间比甲单独完成此项工作所用时间少12天.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 空气污染指数 | 0~50 | 51~100 | 101~150 | 151~200 | 201~250 | 300以上 |
| 空气质量级别 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 严重污染 |
| 天 数 | 6 | 12 | 5 | 4 | 2 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,A、C两点的坐标分别是A(0,4),C(8,0),以OA、OC为邻边作矩形OABC,然后以AC为折痕折叠矩形,使B点落在第四象限的E处,AE交x轴于D点,连接CE并延长交y轴于F点.
如图,平面直角坐标系中,A、C两点的坐标分别是A(0,4),C(8,0),以OA、OC为邻边作矩形OABC,然后以AC为折痕折叠矩形,使B点落在第四象限的E处,AE交x轴于D点,连接CE并延长交y轴于F点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲,l乙分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象.请你写出一个正确的说法:如答案不唯一,如①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了10分钟就到达培训中心;等..
甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲,l乙分别表示甲、乙两人前往目的地所走的路程s(千米)随时间t(分)变化的函数图象.请你写出一个正确的说法:如答案不唯一,如①乙比甲提前12分钟到达;②甲的平均速度为15千米/小时;③乙走了10分钟就到达培训中心;等..查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com