练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知△ABE≌△ACD．

    （1）如果BE=6，DE=2，求BC的长；

    （2）如果∠BAC=75°，∠BAD=30°，求∠DAE的度数．

    【答案】（1）10；（2）15°

    【解析】

    （1）根据全等三角形的性质，可得出BE=CD，根据BE=6，DE=2，得出CE=4，从而得出BC的长；

    （2）根据全等三角形的性质可得出∠BAE=∠CAD，即可得出∠BAD=∠CAE，计算∠CAD﹣∠CAE即得出答案．

    解：（1）∵△ABE≌△ACD，

    ∴BE=CD，∠BAE=∠CAD，

    又∵BE=6，DE=2，

    ∴EC=DC﹣DE=BE﹣DE=4，

    ∴BC=BE+EC=10；

    （2）∠CAD=∠BAC﹣∠BAD=75°﹣30°=45°，

    ∴∠BAE=∠CAD=45°，

    ∴∠DAE=∠BAE﹣∠BAD=45°﹣30°=15°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知:如图，∠1+ ∠2=180° 以∠A= ∠D.求证:AB//CD.(在每步证明过程后面注明理由)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用若干个形状、大小完全相同的矩形纸片围成正方形，4个矩形纸片围成如图①所示的正方形，其阴影部分的面积为12；8个矩形纸片围成如图②所示的正方形，其阴影部分的面积为8；12个矩形纸片围成如图③所示的正方形，其阴影部分的面积为__．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

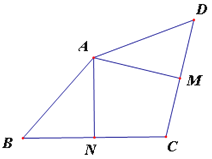
    【题目】如图，在四边形ABCD中，M，N分别是CD，BC的中点，且AM⊥CD，AN⊥BC。

    （1）求证：∠BAD=2∠MAN；

    （2）连接BD，若∠MAN=70°，∠DBC=40°，求∠ADC。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

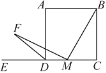
    【题目】如图，在正方形ABCD中，AB＝2，点M为正方形ABCD的边CD上的动点(与点C，D不重合)，连接BM，作MF⊥BM，与正方形ABCD的外角∠ADE的平分线交于点F.设CM＝x，△DFM的面积为y，则y与x之间的函数关系式为________________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息．已知甲先出发4分钟．在整个步行过程中，甲、乙两人的距离y（米）与甲出发的时间t

    （分）之间的关系如图所示，下列结论：

    ①甲步行的速度为60米/分；

    ②乙走完全程用了30分钟；

    ③乙用16分钟追上甲；

    ④乙到达终点时，甲离终点还有320米

    其中正确的结论有（　　）

    A. 1 个B. 2 个C. 3 个D. 4 个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，对于点P (x，y)，若点Q的坐标为(ax+y，x+ay)， 其中a为常数，则称点Q是点P的“a级关联点"，例如，点P(1，4)的“3级关联点"为Q (3×1+4，1+3×4)， 即Q (7，13)。

    (1)已知点A (-2，6)的“级关联点”是点A1，点B的“2级关联点”是B1 (3， 3)， 求点A1和点B的坐标：

    (2)已知点M (m-1， 2m)的“-3级关联点"M位于坐标轴上，求M的坐标

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,抛物线y=-x2+x+与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.

    (1)求点A,B,C的坐标;

    (2)若该抛物线的顶点是点D,求四边形OCDB的面积;

    (3)已知点P是该抛物线对称轴的一点,若以点P,O,D为顶点的三角形是等腰三角形,请直接写出点P的坐标.(不用说理)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

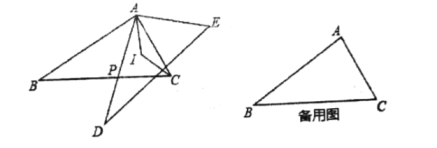
    【题目】如图，△ABC和△ADE中，，，边AD与边BC交于点P（不与点B，C重合），点B，E在AD异侧，AI、CI分别平分，．

    （1）求证：；

    （2）设，请用含的式子表示PD，并求PD的最大值；

    （3）当时，的取值范围为，分别直接写出m，n的值．

    查看答案和解析>>

    同步练习册答案