
 ČēĶ¼£¬ŌŚRt”÷ABO ÖŠ£¬AO=4£¬BO=3£¬¶ÆµćP“ÓAµć³ö·¢£¬ŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶ČŃŲAO·½ĻņĻņµćOŌČĖŁŌĖ¶Æ£¬Ķ¬Ź±¶ÆµćQ“ÓBµć³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŃŲBA·½ĻņĻņµćAŌČĖŁŌĖ¶Æ£¬µ±Ņ»øöµćĶ£Ö¹ŌĖ¶Æ£¬ĮķŅ»øöµćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£¬Į¬½ÓPQ£¬ÉčŌĖ¶ÆŹ±¼äĪŖt£Øs£©£®
ČēĶ¼£¬ŌŚRt”÷ABO ÖŠ£¬AO=4£¬BO=3£¬¶ÆµćP“ÓAµć³ö·¢£¬ŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶ČŃŲAO·½ĻņĻņµćOŌČĖŁŌĖ¶Æ£¬Ķ¬Ź±¶ÆµćQ“ÓBµć³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŃŲBA·½ĻņĻņµćAŌČĖŁŌĖ¶Æ£¬µ±Ņ»øöµćĶ£Ö¹ŌĖ¶Æ£¬ĮķŅ»øöµćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£¬Į¬½ÓPQ£¬ÉčŌĖ¶ÆŹ±¼äĪŖt£Øs£©£®·ÖĪö £Ø1£©×÷QH”ĶOAÓŚH£®Ņ×ÖŖS=$\frac{1}{2}$•AP•QH=$\frac{1}{2}$•2t•$\frac{3}{5}$£Ø5-t£©=-$\frac{3}{5}$t2+3t£¬øł¾Ż¶ž“ĪŗÆŹżµÄŠŌÖŹ¼“æɽā¾öĪŹĢā£»
£Ø2£©ŅņĪŖ”ĻPAQ=”ĻOAB£¬ĖłŅŌµ±$\frac{AP}{AO}$=$\frac{AQ}{AB}$Ź±£¬”÷APQ”×”÷AOB£¬»ņ$\frac{PA}{AB}$=$\frac{AQ}{OA}$Ź±£¬”÷PAQ”×”÷BAO£¬·Ö±šĮŠ³ö·½³Ģ¼“æɽā¾öĪŹĢā£»
£Ø3£©ČēĶ¼2ÖŠ£¬ÉčOPĪŖÖ±¾¶µÄ”ŃKÓėABĻąĒŠÓŚµćM£®Ēó³ö“ĖŹ±µÄtµÄÖµ¼“æɽā¾öĪŹĢā£»
½ā“š ½ā£ŗ£Ø1£©×÷QH”ĶOAÓŚH£®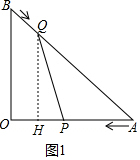
ŌŚRt”÷AOBÖŠ£¬AB=$\sqrt{A{O}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5£¬
”ßQH”ĪOB£¬
”ą$\frac{QH}{OB}$=$\frac{AQ}{AB}$£¬
”ąQH=$\frac{3}{5}$£Ø5-t£©£¬
”ąS=$\frac{1}{2}$•AP•QH=$\frac{1}{2}$•2t•$\frac{3}{5}$£Ø5-t£©=-$\frac{3}{5}$t2+3t£¬
”ßS=-$\frac{3}{5}$£Øt-$\frac{5}{2}$£©2+$\frac{15}{4}$£¬
”ß-$\frac{3}{5}$£¼0£¬0£¼t”Ü2£¬
”ąt=2Ź±£¬SÓŠ×ī“óÖµ£®
£Ø2£©ŅņĪŖ”ĻPAQ=”ĻOAB£¬
ĖłŅŌµ±$\frac{AP}{AO}$=$\frac{AQ}{AB}$Ź±£¬”÷APQ”×”÷AOB£¬
”ą$\frac{2t}{4}$=$\frac{5-t}{5}$£¬
½āµĆt=$\frac{10}{7}$s£¬
»ņ$\frac{PA}{AB}$=$\frac{AQ}{OA}$Ź±£¬”÷PAQ”×”÷BAO£¬
”ą$\frac{2t}{5}$=$\frac{5-t}{4}$£¬
½āµĆt=$\frac{25}{13}$s
×ŪÉĻĖłŹö£¬t=$\frac{10}{7}$s»ņ$\frac{25}{13}$sŹ±Āś×ćĢõ¼ž£®
£Ø2£©ČēĶ¼2ÖŠ£¬ÉčOPĪŖÖ±¾¶µÄ”ŃKÓėABĻąĒŠÓŚµćM£®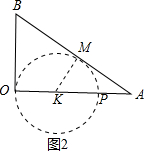
ÓÉsinA=$\frac{KM}{AK}$=$\frac{OB}{AB}$£¬æɵĆ$\frac{\frac{4-2t}{2}}{\frac{4-2t}{2}+2t}$=$\frac{3}{5}$£¬
½āµĆt=$\frac{1}{2}$s£¬
”ąµ±0£¼t£¼$\frac{1}{2}$Ź±£¬”ŃKÓėABĻą½»£¬µ±t=$\frac{1}{2}$Ź±£¬”ŃKÓėABĻąĒŠ£¬µ±$\frac{1}{2}$£¼t£¼2Ź±£¬”ŃKÓėABĻąĄė£®
µćĘĄ ±¾Ģāæ¼²éĻąĖĘŠĪ×ŪŗĻĢā”¢¶ž“ĪŗÆŹż”¢Ō²ÓėÖ±ĻßµÄĪ»ÖĆ¹ŲĻµµČÖŖŹ¶£¬½āĢāµÄ¹Ų¼üŹĒѧ»į¹¹½Ø¶ž“ĪŗÆŹż½ā¾ö×īÖµĪŹĢā£¬Ń§»įÓĆ·ÖĄąĢÖĀŪµÄĖ¼ĻėĖ¼æ¼ĪŹĢā£¬ŹōÓŚÖŠæ¼Ń¹ÖįĢā£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 110”ć | B£® | 125”ć | C£® | 130”ć | D£® | 140”ć |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 1 | B£® | 5 | C£® | -1 | D£® | -5 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
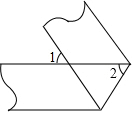 ČēĶ¼½«Ņ»ĢõĮ½±ß¶¼»„ĻąĘ½ŠŠµÄÖ½“ų½ųŠŠÕŪµž£¬Éč”Ļ1ĪŖ¦Į¶Č£¬Ōņ”Ļ2=90”ć-$\frac{1}{2}$¦Į£®£ØĒėÓĆŗ¬ÓŠ¦ĮµÄ“śŹżŹ½±ķŹ¾£©
ČēĶ¼½«Ņ»ĢõĮ½±ß¶¼»„ĻąĘ½ŠŠµÄÖ½“ų½ųŠŠÕŪµž£¬Éč”Ļ1ĪŖ¦Į¶Č£¬Ōņ”Ļ2=90”ć-$\frac{1}{2}$¦Į£®£ØĒėÓĆŗ¬ÓŠ¦ĮµÄ“śŹżŹ½±ķŹ¾£©²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
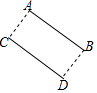 ČēĶ¼ĖłŹ¾£¬Ę½ŅĘĻ߶ĪABµ½CDµÄĪ»ÖĆ£¬ŌņAB=CD£¬CD”ĪAB£¬BD=AC£®
ČēĶ¼ĖłŹ¾£¬Ę½ŅĘĻ߶ĪABµ½CDµÄĪ»ÖĆ£¬ŌņAB=CD£¬CD”ĪAB£¬BD=AC£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com