[题目]如图.将半径为6的⊙O沿AB折叠.弧AB与AB垂直的半径OC交于点D且CD=2OD.则折痕AB的长为( )A. B.C.6 D. 题目和参考答案——青夏教育精英家教网—

【题目】如图，将半径为6的⊙O沿AB折叠，弧AB与AB垂直的半径OC交于点D且CD=2OD，则折痕AB的长为（）

A.　　
B.
C.6　　　
D.

【答案】B
【解析】延长CO交AB于E点，连接OB，构造直角三角形，然后再根据勾股定理求出AB的长。
延长CO交AB于E点，连接OB，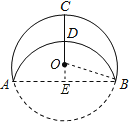

∵CE⊥AB，
∴E为AB的中点，
∵OC=6，CD=2OD，
∴CD=4，OD=2，OB=6，
∴DE=（2OC-CD)=（6×2-4)=×8=4，
∴OE=DE-OD=4-2=2，
在Rt△OEB中，
∵OE2+BE2=OB2
∴
∴AB=2BE=
故选B.
【考点精析】本题主要考查了勾股定理的概念和垂径定理的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧才能正确解答此题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，抛物线y=﹣ x2+mx+n与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．

（1）求抛物线的表达式；
（2）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；
（3）点E是线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，四边形CDBF的面积最大？求出四边形CDBF的最大面积及此时E点的坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在长方形ABCD中，AB=2，BC=1，动点P从点B出发，沿路线B→C→D做匀速运动，那么△ABP的面积S与点P运动的路程x之间的函数图象大致为（）

A.
B.
C.
D.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在平面上，Rt△ABC与直径为CE的半圆O，如图1摆放，∠B=90°，BC=m，AC=2CE=n，半圆O交BC边于点D，将半圆O绕点C按逆时针方向旋转，点D随半圆O旋转，且∠ECD=∠ACB，旋转角记为α（0°≤α≤180°）．
（1）①当α=0°时，连接DE，则∠CDE=°，CD=；②当α=180°时， = ．
（2）试判断：旋转过程中的大小有无变化？请仅就图2的情形给出证明．
（3）若m=4，n=5，当α=∠ACB时，线段BD= ．
（4）若m=4 ，n=6，当半圆O旋转至与△ABC的边相切时，线段BD= ．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知正方形ABCD和正方形AEFG有公共顶点A，将正方形AEFG绕点A旋转．

（1）发现：如图1，当E点旋转到DA的延长线上时，△ABE与△ADG的面积关系是：；
（2）引申：当正方形AEFG旋转任意一个角度时，△ABE与△ADG的面积关系是：；
（3）如图3，四边形ABMN、四边形DEAC、四边形BFGC均为正方形，则S△ABC、S△AEN、S△BMF、S△DCG的关系是；
（4）运用：某小区中有一块空地，要在其中建三个正方形健身场所（如图3），其余空地修成草坪．若已知其中一个正方形的边长为5m，另一个正方形的边长为4m，则草坪的最大面积是．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】抛物线y=﹣x2+4ax+b（a＞0）与x轴相交于O、A两点（其中O为坐标原点），过点P（2，2a）作直线PM⊥x轴于点M，交抛物线于点B，点B关于抛物线对称轴的对称点为C（其中B、C不重合），连接AP交y轴于点N，连接BC和PC．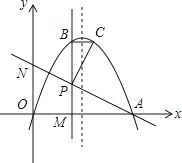

（1）a= 时，求抛物线的解析式和BC的长；
（2）如图a＞1时，若AP⊥PC，求a的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的，她先用尺规作出了如图1的四边形ABCD，并写出了如下不完整的已知和求证．
已知：如图1，在四边形ABCD中，BC=AD，

求证：四边形ABCD是四边形．
（1）在方框中填空，以补全已知和求证；
（2）按嘉淇的想法写出证明；
（3）用文字叙述所证命题的逆命题为平行四边形两组对边分别相等