
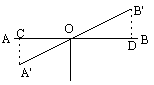
如图所示,铁道口的栏杆的短臂OA长1.25米,长臂OB长16.5米,当短臂端点A下降0.85米时,长臂端点升高多少(杆的高度可忽略不计)?
科目:初中数学 来源: 题型:
| 1 |
| 3 |
| 5 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:新课标读想练同步测试 八年级数学(下) 题型:044
已知:如图所示,铁道口的栏杆的短臂长1.25m,长臂长16.5m,当短臂端点A下降0.85m时,长臂端点B升高多少米(杆的宽度忽略不计)?

查看答案和解析>>
科目:初中数学 来源:101网校同步练习 初二数学 人教版(新课标2004年初审) 人教版(新课标2004年初审) 题型:044
如图所示.铁道口的栏杆的短臂长1.25米,长臂长16.5米,当短臂端点下降0.85米时,长臂端点升高多少米?(杆的宽度忽略不计)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com