练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在数学课上，老师提出如下问题：

    如图，已知线段AB，BC，∠ABC = 90°. 求作：矩形ABCD.

    小明的作图过程如下：

    （1）连接AC，作线段AC的垂直平分线，交AC于M;

    （2）连接BM并延长，在延长线上取一点D，使MD=MB，连接AD，CD.

    ∴四边形ABCD即为所求.

    老师说：“小明的作法正确．”

    请回答：小明这样作图的依据是______.

    【答案】有一个角是90°的平行四边形是矩形（或对角线互相平分且相等的四边形是矩形）

    【解析】

    第（1）步作图得到AC中点，第（2）步根据平行四边形对角线互相平分取点D，所得图形为矩形.

    解：因为∠ABC = 90°，满足有一个角为直角，根据矩形对角线互相平分，

    连接AC，作线段AC的垂直平分线，交AC于M，可得四边形是平行四边形，

    所以所作图形为矩形.

    故答案为：有一个角是90°的平行四边形是矩形（或对角线互相平分且相等的四边形是矩形）.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，点D是斜边AB的中点，过点B、点C分别作BE∥CD，CE∥BD.

    （1）求证：四边形BECD是菱形；

    （2）若∠A=60°，AC=，求菱形BECD的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）.

    (1) 请画出△ABC向左平移5个单位长度后得到的△ABC；

    (2) 请画出△ABC关于原点对称的△ABC；

    (3) 在轴上求作一点P，使△PAB的周长最小，请画出△PAB，并直接写出P的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

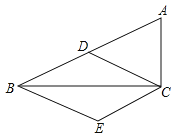
    【题目】我们不妨约定：如图①，若点D在△ABC的边AB上，且满足∠ACD=∠B（或∠BCD=∠A），则称满足这样条件的点为△ABC边AB上的“理想点”．

    （1）如图①，若点D是△ABC的边AB的中点，AC=，AB=4.试判断点D是不是△ABC边AB上的“理想点”，并说明理由．

    （2）如图②，在⊙O中，AB为直径，且AB=5，AC=4.若点D是△ABC边AB上的“理想点”，求CD的长．

    （3）如图③，已知平面直角坐标系中，点A(0,2),B(0,-3),C为x轴正半轴上一点，且满足∠ACB=45°，在y轴上是否存在一点D，使点A是B，C，D三点围成的三角形的“理想点”，若存在，请求出点D的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

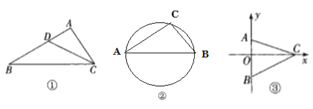
    【题目】如图，以AB边为直径的⊙O经过点P，C是⊙O上一点，连结PC交AB于点E，且∠ACP=60°，PA=PD．

    （1）试判断PD与⊙O的位置关系，并说明理由；

    （2）若点C是弧AB的中点，已知AB=4，求CECP的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与探究

    如图，抛物线y=－x2+bx+c与x轴交于A（－1，0），B两点，与y轴交于点C，对称轴为x=1．

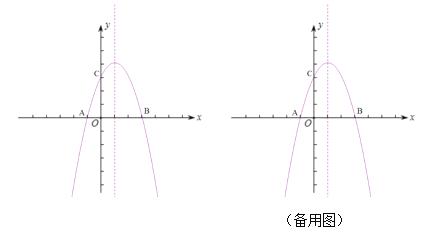
    （1）求抛物线的函数表达式；

    （2）在抛物线的对称轴上求一点P，使点P到点A的距离与到点C的距离之和最小，并求出此时点P的坐标；

    （3）是否存在过A，B两点的抛物线，其顶点M关于x轴的对称点为N，使得四边形AMBN为正方形？若存在，请直接写出此抛物线的函数表达式；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2018年10月21日，重庆市第八届中小学艺术工作坊在渝北区空港新城小学体育馆开幕，来自全重庆市各个区县共二十多个工作坊集中展示了自己的艺术特色．组委会准备为现场展示的参赛选手购买三种纪念品，其中甲纪念品5元/件，乙纪念品7元/件，丙纪念品10元/件．要求购买乙纪念品数量是丙纪念品数量的2倍，总费用为346元．若使购买的纪念品总数最多，则应购买纪念品共_____件．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y＝ax2＋bx＋c（a＜0＜b）的图像与x轴只有一个交点，下列结论：①x＜0时，y随x增大而增大；②a＋b＋c＜0；③关于x的方程ax2＋bx＋c＋2＝0有两个不相等的实数根．其中所有正确结论的序号是（ ）

    A.①②B.②③C.①③D.①②③

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PA，PB，AB，已知∠PBA=∠C．

    （1）求证：PB是⊙O的切线；

    （2）连接OP，若OP∥BC，且OP=8，⊙O的半径为，求BC的长．

    查看答案和解析>>

    同步练习册答案