
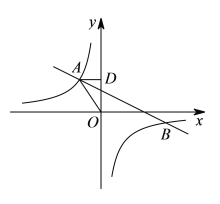
【题目】如图,在平面直角坐标系xOy中,Rt△OCD的一边OC在x轴上,∠OCD=90°,点D在第一象限,OC=6,DC=4,反比例函数的图象经过OD的中点A.
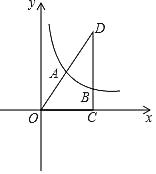
(1)求该反比例函数的解析式;
(2)若该反比例函数的图象与Rt△OCD的另一边DC交于点B,求过A、B两点的直线的解析式.
 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是的直径,PA与⊙O 相切于点A,点C在⊙O 上,且PC=PA,
(1)求证PC是⊙O的切线;
(2)过点C作CD⊥AB于点E,交⊙O于点D,若CD=PA=2![]() ,
,
①求图中阴影部分面积;
②连接AC,若△PAC的内切圆圆心为I,则线段IE的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
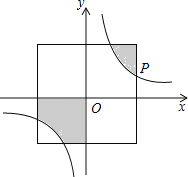
【题目】如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(3a,a)是反比例函数![]() (k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为 ▲ .
(k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为 ▲ .
查看答案和解析>>
科目:初中数学 来源: 题型:
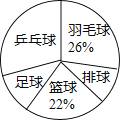
【题目】某中学为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1800名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种),调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 | a | b | 33 | 21 |
解答下列问题:
(1)这次抽样调查的总人数是 ,统计表中a的值为 .
(2)求扇形统计图中排球一项的扇形圆心角度数.
(3)试估计全校1800名学生中最喜欢乒乓球运动的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
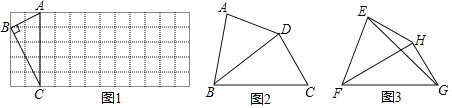
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数![]()
![]() 与一次函数
与一次函数![]() 交于第二、四象限的
交于第二、四象限的![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求反比例函数和一次函数的解析式;
(2)请根据图象直接写出![]() 的自变量
的自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+2经过A(﹣1,0),B(2,0),C三点.直线y=mx+![]() 交抛物线于A,Q两点,点P是抛物线上直线AQ上方的一个动点,作PF⊥x轴,垂足为F,交AQ于点N.
交抛物线于A,Q两点,点P是抛物线上直线AQ上方的一个动点,作PF⊥x轴,垂足为F,交AQ于点N.

(1)求抛物线的解析式;
(2)如图①,当点P运动到什么位置时,线段PN=2NF,求出此时点P的坐标;
(3)如图②,线段AC的垂直平分线交x轴于点E,垂足为D,点M为抛物线的顶点,在直线DE上是否存在一点G,使△CMG的周长最小?若存在,请求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com