
 在正方形ABCD中,点E在BC的延长线上,且CE=CD,点F为DE边上一点,连接AF,作FG⊥AF交直线DC于点G
在正方形ABCD中,点E在BC的延长线上,且CE=CD,点F为DE边上一点,连接AF,作FG⊥AF交直线DC于点G分析 (1)先判断出,∠ADF=∠GCF,进而得出,△ADF≌△GCF即可得出结论;
(2)构造全等三角形,同(1)的方法判断出,△ADF≌△GHF,再出AD=HG最后用等量代换即可.
解答 解:(1)等腰直角三角形,理由如下:
如图1,连接CF,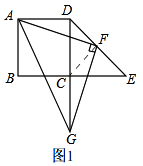
在Rt△CDE中,CE=CD,DF=EF,
∴CF=DF=EF,∠ECF=∠CDE=45°,
∴∠ADF=∠ADC+∠CDF=135°,∠FCG=∠GCE+∠ECF=135°,
∴∠ADF=∠GCF,
∵AF⊥FG,HF⊥DE,
∴∠AFG=∠DFH=90,
∴∠AFD=∠GFH
在△ADF和△GCF中,$\left\{\begin{array}{l}{∠DAF=∠CGF}\\{∠AFD=∠GFC}\\{DF=FC}\end{array}\right.$,
∴△ADF≌△GCF(AAS),
∴AF=FG,
∵∠AFG=90°,
∴△AFG是等腰直角三角形.
(2)DG=AD+$\sqrt{2}$DF;
理由:如图2,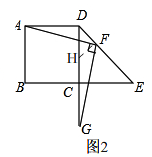 过点F作FH⊥DE,
过点F作FH⊥DE,
由(1)知,∠CDE=45°,
∴DH=$\sqrt{2}$DF,DF=HF,∠DHF=45°,
同(1)的方法得出∠ADF=∠GHF
在△ADF和△GHF中,$\left\{\begin{array}{l}{∠DAF=∠HGF}\\{∠ADF=∠GHF}\\{DF=HF}\end{array}\right.$,
∴△ADF≌△GHF(AAS),
∴AD=HG,
∴DG=DH+HG=$\sqrt{2}$DF+AD.
点评 主要考查了正方形的性质,矩形的性质,等腰三角形的性质,全等三角形的判定和性质,解本题的关键是,△ADF≌△GHF.


科目:初中数学 来源:2016-2017学年贵州省七年级下学期第一次月考数学试卷(解析版) 题型:解答题
如图所示,在长和宽分别是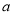 、
、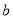 的矩形纸片的四个角都剪去一个边长为
的矩形纸片的四个角都剪去一个边长为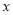 的小正方形.
的小正方形.

(1)用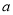 、
、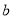 、
、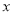 表示纸片剩余部分的面积;
表示纸片剩余部分的面积;
(2)当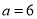 ,
, 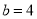 ,且剪去部分的面积等于剩余部分的面积时,求正方形的边长
,且剪去部分的面积等于剩余部分的面积时,求正方形的边长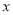 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
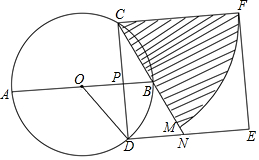 如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为P,BP:PA=1:3,CD=2$\sqrt{3}$.
如图,AB是⊙O的直径,CD是⊙O的弦,AB⊥CD,垂足为P,BP:PA=1:3,CD=2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
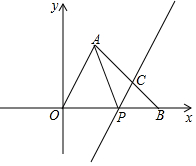 如图,将△OAB放在平面直角坐标系中,O为原点,点A(2,4),点B(6,0)在边OB上有一动点P,过P作PC∥OA交AB于C,连接AP.
如图,将△OAB放在平面直角坐标系中,O为原点,点A(2,4),点B(6,0)在边OB上有一动点P,过P作PC∥OA交AB于C,连接AP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
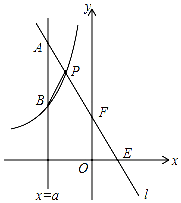 如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{4}{x}$
如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{4}{x}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com