
����Ŀ���������и�����������ABC���A1B1C1���Ƶ���( )
�١�A��45����AB��12��AC��15����A1��45����A1B1��16��A1C1��20
��AB��12��BC��15��AC��24��A1B1��20��A1C1��40��B1C1��25
�ۡ�B����B1��75������C��50������A1��55��
�ܡ�C����C1��90����AB��10��AC��6��A1B1��15��A1C1��9
A. 1�� B. 2�� C. 3�� D. 4��
���𰸡�D
��������
������Ҫ�������������ε��ж��������н��
�����һ�������ε�����������һ�������ε������Ƕ�Ӧ��ȣ���ô���������������ƣ�
��������������ε������Ӧ�ߵı���ȣ�������Ӧ�ļн���ȣ���ô���������������ƣ�
��������������ε������Ӧ�ߵı���ȣ���ô���������������ƣ�
�⣺�ٷ��������Ӧ�ߵı��������Ӧ�ļн���ȵ��������������ƣ���ѡ����ȷ��
�ڷ��������Ӧ�ߵı���ȵ��������������ƣ���ѡ����ȷ��
�۷���������Ƕ�Ӧ��ȵ��������������ƣ���ѡ����ȷ��
�����ù��ɶ�������BC��8��B1C1��12�����������Ӧ�ߵıȶ���![]() ����ѡ����ȷ��
����ѡ����ȷ��
��ѡ��D��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ACB��90����OC��2BO��AC��6����B������Ϊ��1��0����������y����x2+bx+c����A��B���㣮
��1�����A�����ꣻ
��2���������ߵĽ���ʽ��
��3����P��ֱ��AB�Ϸ��������ϵ�һ�㣬����P��PD��ֱx���ڵ�D�����߶�AB�ڵ�E��ʹPE��![]() DE��
DE��
�����P�����ꣻ
����ֱ��PD���Ƿ���ڵ�M��ʹ��ABMΪֱ�������Σ������ڣ�����������������е�M�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB����O��ֱ����D��E�ǰ�Բ���������㣬����AD��DE��AE��BD�ཻ�ڵ�C��Ҫʹ��ADC����BDA���ƣ���������һ���������������ӵ������д������( )

A. ��ACD����DAB B. AD��DE C. AD��AB��CD��BD D. AD2��BD��CD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
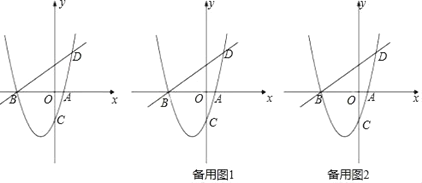
����Ŀ��(12��)��ͼ����֪������y��ax2+bx��2(a��0)��x�ύ��A��B���㣬��y�ύ��C�㣬ֱ��BD���������ڵ�D������D(2��3)��B(��4��0)��
(1)�������ߵĽ���ʽ��
(2)��֪��MΪ��������һ���㣬���ڵ������ޣ�˳�����ӵ�B��M��C�����BMC��������ֵ��
(3)��(2)�С�BMC������������£�����M��ֱ��ƽ����y�ᣬ������ֱ�����Ƿ����һ����Q��ΪԲ�ģ�OQΪ�뾶����ֱ��AC���е�Բ�������ڣ����Բ��Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ijУ���и��꼶ѧ��ÿ���ƽ��˯��ʱ�䣨��λ��h����ȷ��1h�������������˲���ѧ�������õõ������ݻ���������������������ͳ��ͼ��
�������ͼ���ṩ����Ϣ���ش��������⣺
��1���������ͳ��ͼ�аٷ���a��ֵΪ�� ����������ѧ������Ϊ�� ����
��2�����ƽ��˯��ʱ��Ϊ8Сʱ������������ȫƵ��ֱ��ͼ��
��3������ⲿ��ѧ����ƽ��˯��ʱ���������ƽ������
��4�������У����ѧ��1200�����������˯�߲��㣨����8Сʱ����ѧ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)����������������Ľ���Ϊ���㣬�ֱ��������ƱȲ�Ϊ1�����������Σ�ʹ���ǣ��ٶ���ֱ�������Σ��ڶ�����������Σ��۶��Ƕ۽������Σ�
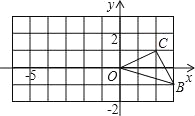
(2)��ͼ����֪O������ԭ�㣬B��C���������ֱ�Ϊ(3����1)��(2��1)��
����0��Ϊλ��������y�����ཫ��OBC�Ŵ�����(����ͼ��ԭͼ�����Ʊ�Ϊ2)������ͼ�Σ�
�ڷֱ�д��B��C����Ķ�Ӧ��B����C�������ꣻ
�������OBC�ڲ�һ��M������Ϊ(x��y)��д��M�Ķ�Ӧ��M�������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���![]() �У�
��![]() ��
��![]() cm������
cm������![]() ��2cm/s���ٶ���
��2cm/s���ٶ���![]() �ı�����
�ı�����![]() �ķ��������˶�������
�ķ��������˶�������![]() ��
��![]() �ı�����
�ı�����![]() �ķ��������˶���
�ķ��������˶���![]() ��
��![]() ����ͬʱ������5s��
����ͬʱ������5s��![]() �����յ�
�����յ�![]() ����
����![]() ����ֹͣ�˶�(��ʱ��
����ֹͣ�˶�(��ʱ��![]() ��δ�����
������![]() ).���
).���![]() �˶���ʱ��Ϊ
�˶���ʱ��Ϊ![]() (s)��
(s)��![]() �����Ϊ
�����Ϊ![]() (cm2)��
(cm2)��![]() ��
��![]() �ĺ���ͼ����ͼ����ʾ.
�ĺ���ͼ����ͼ����ʾ.
(1)ͼ����![]() cm����
cm����![]() �˶����ٶ�Ϊ cm/s;
�˶����ٶ�Ϊ cm/s;
(2)����![]() �����ֵ;
�����ֵ;
(3)��![]() Ϊ��ֵʱ����
Ϊ��ֵʱ����![]() ��
��![]() ��
��![]() �������������
Ϊ�������������![]() ����?��˵������.
����?��˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
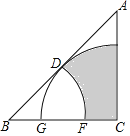
����Ŀ����ͼ����֪����ֱ��������ABC����ACB=90����D��б��AB���е㣬��AC=BC=16���ף��Ե�BΪԲ�ģ�BDΪ�뾶��������BC�ڵ�F���Ե�CΪԲ�ģ�CDΪ�뾶�������ֱ�AB��BC�ڵ�E��G������Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��3x2��36x��81.
(1)д�����Ķ������ꣻ
(2)��xȡ��ֵʱ��y��x�����������
(3)���ͼ����x��Ľ������ꣻ
(4)��xȡ��ֵʱ��y����Сֵ���������Сֵ��
(5)��xȡ��ֵʱ��y��0.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com