
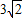 Ł¬AN=
Ł¬AN=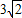 Ł¬AD=2Ł¬CN=2Ł¬¸ůľÝĆ˝ĐĐËıßĐεÄĹж¨¶¨ŔíżÉµĂËıßĐÎCDANĘÇĆ˝ĐĐËıßĐÎŁ»
Ł¬AD=2Ł¬CN=2Ł¬¸ůľÝĆ˝ĐĐËıßĐεÄĹж¨¶¨ŔíżÉµĂËıßĐÎCDANĘÇĆ˝ĐĐËıßĐÎŁ»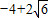 Ł©»ňŁ¨1Ł¬
Ł©»ňŁ¨1Ł¬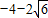 Ł©Ł®
Ł©Ł®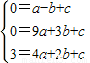 Ł¬
Ł¬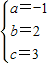
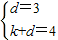 Ł¬
Ł¬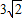 Ł¬AN=
Ł¬AN= Ł¬AD=2Ł¬CN=2
Ł¬AD=2Ł¬CN=2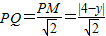 Ł¬
Ł¬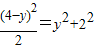 Ł¬
Ł¬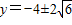 Ł¬·űşĎĚâŇ⣬
Ł¬·űşĎĚâŇ⣬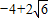 Ł©»ňŁ¨1Ł¬
Ł©»ňŁ¨1Ł¬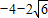 Ł©Ł®
Ł©Ł®

 Őă´óÓĹѧСѧÄ꼶Ďνӽݾ¶Őă˝´óѧłö°ćÉçϵÁĐ´đ°¸
Őă´óÓĹѧСѧÄ꼶Ďνӽݾ¶Őă˝´óѧłö°ćÉçϵÁĐ´đ°¸
| Ä꼶 | ¸ßÖĐżÎłĚ | Ä꼶 | łőÖĐżÎłĚ |
| ¸ßŇ» | ¸ßŇ»Ăâ·ŃżÎłĚÍĆĽöŁˇ | łőŇ» | łőŇ»Ăâ·ŃżÎłĚÍĆĽöŁˇ |
| ¸ß¶ţ | ¸ß¶ţĂâ·ŃżÎłĚÍĆĽöŁˇ | łő¶ţ | łő¶ţĂâ·ŃżÎłĚÍĆĽöŁˇ |
| ¸ßČý | ¸ßČýĂâ·ŃżÎłĚÍĆĽöŁˇ | łőČý | łőČýĂâ·ŃżÎłĚÍĆĽöŁˇ |
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
| 5 |
| 2 |
| 13 |
| 4 |
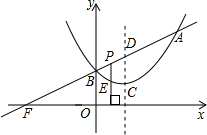 Čý˝ÇĐÎÓëˇ÷BOFĎŕËĆŁżČô´ćÔÚŁ¬ÇëÇółöPµăµÄ×ř±ęŁ»Čô˛»´ćÔÚŁ¬Çë˵Ă÷ŔíÓÉŁ®
Čý˝ÇĐÎÓëˇ÷BOFĎŕËĆŁżČô´ćÔÚŁ¬ÇëÇółöPµăµÄ×ř±ęŁ»Čô˛»´ćÔÚŁ¬Çë˵Ă÷ŔíÓÉŁ®˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
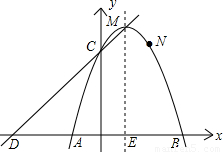
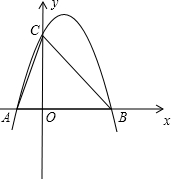
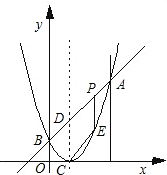 ČçÍĽŁ¬ŇŃÖŞ¶ţ´ÎşŻĘýÍĽĎóµÄ¶Ąµă×ř±ęÎŞCŁ¨1Ł¬0Ł©Ł¬Ö±Ďßy=x+bÓë¸Ă¶ţ´ÎşŻĘýµÄÍĽĎó˝»ÓÚAˇ˘BÁ˝µăŁ¬ĆäÖеăAµÄ×ř±ęÎŞŁ¨3Ł¬4Ł©Ł¬µăBÔÚyÖáÉĎŁ®µăPÎŞĎ߶ÎABÉϵÄŇ»¸ö¶ŻµăŁ¨µăPÓëAˇ˘B˛»Öغϣ©Ł¬ąýµăP×÷xÖáµÄ´ąĎßÓë¸Ă¶ţ´ÎşŻĘýµÄÍĽĎó˝»ÓÚµăEŁ®
ČçÍĽŁ¬ŇŃÖŞ¶ţ´ÎşŻĘýÍĽĎóµÄ¶Ąµă×ř±ęÎŞCŁ¨1Ł¬0Ł©Ł¬Ö±Ďßy=x+bÓë¸Ă¶ţ´ÎşŻĘýµÄÍĽĎó˝»ÓÚAˇ˘BÁ˝µăŁ¬ĆäÖеăAµÄ×ř±ęÎŞŁ¨3Ł¬4Ł©Ł¬µăBÔÚyÖáÉĎŁ®µăPÎŞĎ߶ÎABÉϵÄŇ»¸ö¶ŻµăŁ¨µăPÓëAˇ˘B˛»Öغϣ©Ł¬ąýµăP×÷xÖáµÄ´ąĎßÓë¸Ă¶ţ´ÎşŻĘýµÄÍĽĎó˝»ÓÚµăEŁ®˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
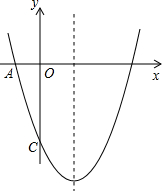 ČçÍĽŁ¬ŇŃÖŞ¶ţ´ÎşŻĘýy=ax2-4x+cµÄÍĽĎóÓë×ř±ęÖá˝»ÓÚµăAŁ¨-1Ł¬0Ł©şÍµăCŁ¨0Ł¬-5Ł©Ł®
ČçÍĽŁ¬ŇŃÖŞ¶ţ´ÎşŻĘýy=ax2-4x+cµÄÍĽĎóÓë×ř±ęÖá˝»ÓÚµăAŁ¨-1Ł¬0Ł©şÍµăCŁ¨0Ł¬-5Ł©Ł®˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
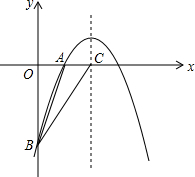 Ł¨2012•şâˮһģŁ©ČçÍĽŁ¬ŇŃÖŞ¶ţ´ÎşŻĘýy=-
Ł¨2012•şâˮһģŁ©ČçÍĽŁ¬ŇŃÖŞ¶ţ´ÎşŻĘýy=-| 1 | 2 |
˛éż´´đ°¸şÍ˝âÎö>>
°Ů¶ČÖÂĐĹ - Á·Ď°˛áÁбí - ĘÔĚâÁбí
şţ±±Ęˇ»ĄÁŞÍřÎĄ·¨şÍ˛»ÁĽĐĹϢľŮ±¨Ć˝Ě¨ | ÍřÉĎÓĐş¦ĐĹϢľŮ±¨×¨Çř | µçĐĹթƾٱ¨×¨Çř | ÉćŔúĘ·ĐéÎŢÖ÷ŇĺÓĐş¦ĐĹϢľŮ±¨×¨Çř | ÉćĆóÇÖȨľŮ±¨×¨Çř
ÎĄ·¨şÍ˛»ÁĽĐĹϢľŮ±¨µç»°Łş027-86699610 ľŮ±¨ÓĘĎ䣺58377363@163.com