
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
 画出函数y=2x-3的图象,并根据图象回答下列问题:
画出函数y=2x-3的图象,并根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 记录数值 | 0 | -7 | +6 | -2 | +8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
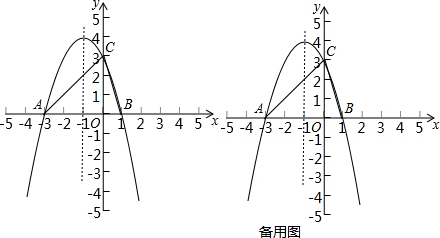
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
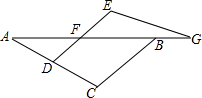 甲、乙两位同学同解一道题目:“如图,F、G是直线AB上的两点,D是AC上的一点,且DF∥CB,∠E=∠C,请写出与△ABC相似的三角形,并加以证明”.
甲、乙两位同学同解一道题目:“如图,F、G是直线AB上的两点,D是AC上的一点,且DF∥CB,∠E=∠C,请写出与△ABC相似的三角形,并加以证明”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
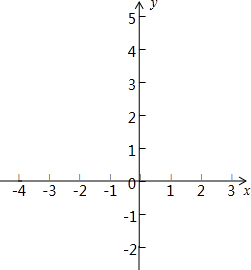 已知关于x的一元二次方程x2+2x+$\frac{k-1}{2}$=0有两个不相等的实数根,k为正整数.
已知关于x的一元二次方程x2+2x+$\frac{k-1}{2}$=0有两个不相等的实数根,k为正整数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
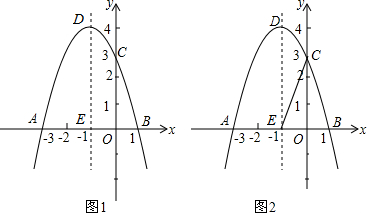
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com