
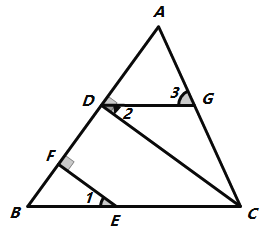
【题目】如图,在△ABC中,CD⊥AB,垂足为D. 点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
(1)试说明DG∥BC的理由;
(2)如果∠B=54°,且∠ACD=35°,求的∠3度数.
【答案】(1)见解析;(2)71°.
【解析】
(1)由CD⊥AB,EF⊥AB即可得出CD∥EF,从而得出∠1=∠BCD,再根据∠1=∠2即可得出∠2=∠BCD,依据“内错角相等,两直线平行”即可证出DG∥BC;
(2)在Rt△BCD中,利用直角三角形的两锐角互余可得到∠BCD的度数,进一步得到∠ACB,再根据BC∥DG即可得出∠3=∠ACB.
(1)证明:∵CD⊥AB,EF⊥AB,
∴∠BFE=∠BDC=90°,
∴CD∥EF,
∴∠1=∠BCD.
又∵∠1=∠2,
∴∠2=∠BCD,
∴DG∥BC.
(2)解:在Rt△BCD中,∠B=54°,
∴∠BCD=90°-54°=36°,
∴∠ACB=∠ACD+∠BCD=35°+36°=71°,
又∵BC∥DE,
∴∠3=∠ACB=71°.


科目:初中数学 来源: 题型:
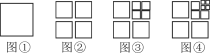
【题目】将图①中的正方形剪开得到图②,图②中共有4个正方形;将图②中一个正方形剪开得到图③,图③中共有7个正方形;将图③中一个正方形剪开得到图④,图④中共有10个正方形……如此下去,则第2018个图中共有正方形的个数为( )
 …
…
A.2018个B.6049个C.6052个D.6055个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.
(1)求证:四边形ABCD是矩形.
(2)若∠ADF:∠FDC=3:2,DF⊥AC,则∠BDF的度数是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,M、N是对角线BD上两点,且BN=DM.
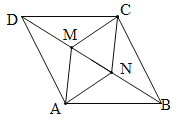
(1)求证:AM=CN;
(2)若AM⊥BD于M,AD=10,CN=6,求DM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠B=60,E是边CD上一点,以CE为边作等边△CEF.
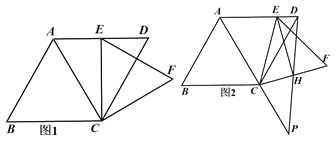
(1) 如图1,当CE⊥AD ,CF=![]() 时,求菱形ABCD的面积;
时,求菱形ABCD的面积;
(2) 如图2,过点E作∠CEF的平分线交CF于H,连接DH,并延长DH与AC的延长交于点P,若∠ECD=15,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知雅美服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M、N两种型号的时装共80套.已知做一套M型号的时装需用A种布料1.1米,B种布料0.4米,可获利50元;做一套N型号的时装需用A种布料0.6米,B种布料0.9米,可获利45元.设生产M型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
(1)求y(元)与x(套)的函数关系式,并求出自变量的取值范围;
(2)当M型号的时装为多少套时,能使该厂所获利润最大?最大利润是多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形纸片ABC中,∠A=90°,∠C=30°,AC=10cm,将该纸片沿过点B的直线折叠,使点A落在斜边BC上的一点E处,折痕记为BD(如图1),剪去△CDE后得到双层△BDE(如图2),再沿着过△BDE某顶点的直线将双层三角形剪开,使得展开后的平面图形中有一个是平行四边形,则所得平行四边形的周长为_____cm.
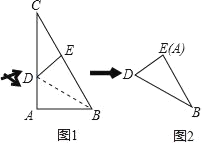
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com