
分析 (1)根据点的坐标,利用待定系数法求出一次函数关系式即可;
(2)将x=4代入一次函数关系式中,求出y值即可.
解答 解:(1)设y与x之间的函数关系式为y=kx+b,
将(0,3)、(2,7)代入y=kx+b,
$\left\{\begin{array}{l}{b=3}\\{2k+b=7}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=2}\\{b=3}\end{array}\right.$,
∴y与x之间的函数关系式为y=2x+3.
(2)当x=4时,y=2x+3=2×4+3=11.
点评 本题考查了待定系数法求一次函数解析式以及一次函数图象上点的坐标特征,解题的关键是:(1)根据点的坐标利用待定系数法求出一次函数关系式;(2)将x=4代入一次函数关系式求出y值.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:解答题
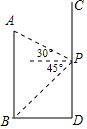 如图,AB、CD分别表示两幢相距36米的大楼,小明同学站在CD大楼的P处窗口观察AB大楼的底部B点的俯角为45°,观察AB大楼的顶部A点的仰角为30°.
如图,AB、CD分别表示两幢相距36米的大楼,小明同学站在CD大楼的P处窗口观察AB大楼的底部B点的俯角为45°,观察AB大楼的顶部A点的仰角为30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
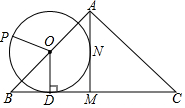 如图,在△ABC中,AB=AC,点O为边AB的中点,OD⊥BC于点D,AM⊥BC于点M,以点O为圆心,线段OD为半径的圆与AM相切于点N.
如图,在△ABC中,AB=AC,点O为边AB的中点,OD⊥BC于点D,AM⊥BC于点M,以点O为圆心,线段OD为半径的圆与AM相切于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
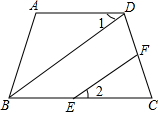 完成下面推理过程.
完成下面推理过程.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2 ).
如图,平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+6,b-2 ).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com