
【题目】已知:如图△ABC中,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O与点F,点E在AC上,且∠EBC= ![]() ∠BAC,BE交⊙O于点D.
∠BAC,BE交⊙O于点D.
(1)求证:AB=AE;
(2)若AB=10,cos∠EBC= ![]() ,求线段BE和BC的长.
,求线段BE和BC的长.
【答案】
(1)
证明:连接AD,
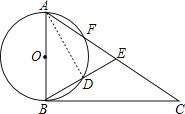
∵AB为直径,
∴∠ADB=90°=∠ADE,
∴∠DAB+∠ABD=90°,
∵BC切⊙O于B,
∴∠ABD+∠EBC=90°,
∴∠EBC=∠BAD,
∵∠EBC= ![]() ∠BAC,
∠BAC,
∴∠EAD=∠BAD,
在△ABD和△AED中

∴△ABD≌△AED(ASA),
∴AB=AE.
(2)
解: 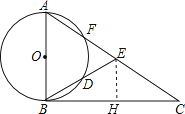 ∵∠EBC=∠BAD,AB=10,cos∠EBC=
∵∠EBC=∠BAD,AB=10,cos∠EBC= ![]() ,
,
∴在Rt△BAD中,cos∠BAD= ![]() =
= ![]() ,
,
∴AD=4 ![]() ,
,
由勾股定理得:BD=2 ![]() ,
,
∵△ABD≌△AED,
∴BD=DE,
∴BE=2BD=4 ![]() ,
,
过E作EH⊥BC于H,
则EH∥AB,
∵cos∠EBC= ![]() ,BE=4
,BE=4 ![]() ,
,
∴BH=BEcos∠EBC=8,
由勾股定理得:EH= ![]() =4,
=4,
∵EH∥AB,
∴△CHE∽△CBA,
∴ ![]()
∴ ![]() ,
,
∴CH=5 ![]() ,
,
∴BC=8+5 ![]() =13
=13 ![]() .
.
【解析】(1)连接AD,求出∠EBC=∠BAD,推出∠BAD=∠EAD,证出△ABD≌△AED即可.(2)根据∠EBC=∠BAD,AB=10,cos∠EBC= ![]() 求出AD,根据勾股定理求出BD,即可求出答案,求出EH,BH,根据相似求出CH,即可求出答案.
求出AD,根据勾股定理求出BD,即可求出答案,求出EH,BH,根据相似求出CH,即可求出答案.
【考点精析】解答此题的关键在于理解切线的性质定理的相关知识,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,AD=2AB,F是AD的中点,作
ABCD中,AD=2AB,F是AD的中点,作![]() ,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )
,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )

①![]() ②EF=CF
②EF=CF
③![]() ④
④![]()
A. ①②③ B. ①② C. ②③ ④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )

A. 2 B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝即将到来的“五四”青年节,某校举行了书法比赛,赛后随机抽查部分参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x≤100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)这次随机抽查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)全校共有600名学生参加比赛,估计该校成绩80≤x<100范围内的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小正方形的边长都是1.A、B、C三点都在格点上.
(1)请你以格线所在直线为坐标轴建立平面直角坐标系,使A、B两点的坐标分别为A(﹣2,3),B(﹣3,1),并写出C点坐标;
(2)连接AB、BC、CA得△ABC,将△ABC向右平移4个单位,画出平移后的△A1B1C1;
(3)将△A1B1C1绕点B1按顺时针方向旋转90°,画出旋转后的△A2B1C2 , 并求出在旋转过程中线段A1B1所扫过的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△PAB的边PA、PB上分别取点C、D,连接CD使CD∥AB.将△PCD绕点P按逆时针方向旋转得到△PC′D′(∠APC′<∠APB),连接AC′、BD′.
(1)如图1, 若∠APB=90°,PA=PB,求证:AC′=BD′;AC′⊥BD′.
(2)在图1中,连接AD′、BC′,分别取AB、AD′、C′D′、BC′的中点E、F、G、H,顺次连接E、F、G、H得到四边形EFGH.请判断四边形EFGH的形状,并说明理由.
(3)①如图2, 若改变(1)中∠APB的大小,使0°<∠APB<90°,其他条件不变,重复(2)中操作.请你直接判断四边形EFGH的形状.
②如图3,若改变(1)中PA、PB的大小关系,使PA<PB,其他条件不变,重复(2)中操作,请你直接判断是四边形EFGH的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸每个小方格是边长为1个单位长度的正方形,在平面直角坐标系中,点A(1,0),B(5,0),C(a,b)D(1,4).
(1)描出A、B、C、D四点的位置.如图,则a= ;b= ;
(2)四边形ABCD的面积是 ;(直接写出结果)
(3)把四边形ABCD向左平移6个单位,再向下平移1个单位得到四边形A'B'C'D',在图中画出四边形A'B'C'D',并写出A'B'C'D'的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com