
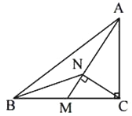
【题目】如图所示,在△ABC中,∠ACB=90°,AM是BC边的中线,CN⊥AM于N点,连接BN,求证:
(1)△MCN∽△MAC;
(2)∠NBM=∠BAM.
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某天猫店销售某种规格学生软式排球,成本为每个30元.以往销售大数据分析表明:当每只售价为40元时,平均每月售出600个;若售价每上涨1元,其月销售量就减少20个,若售价每下降1元,其月销售量就增加200个.
(1)若售价上涨m元,每月能售出 个排球(用m的代数式表示).
(2)为迎接“双十一”,该天猫店在10月底备货1300个该规格的排球,并决定整个11月份进行降价促销,问售价定为多少元时,能使11月份这种规格排球获利恰好为8400元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想了解全校3000名同学对新闻、体育、音乐、娱乐、戏曲五类电视节目的喜爱况,从中抽取了一部分同学进行了一次抽样调查,利用所得数据绘制成下面的统计图:根据图中所给信息,全校喜欢娱乐类节目的学生大约有( )人.
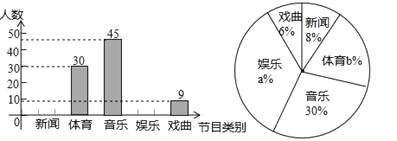
A. 1080 B. 900 C. 600 D. 108
查看答案和解析>>
科目:初中数学 来源: 题型:
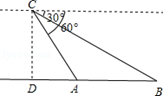
【题目】某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援.当飞机到达距离海面3000米的高空C处,测得A处渔政船的俯角为60°,测得B处发生险情渔船的俯角为30°,请问:此时渔政船和渔船相距多远?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 在正方形ABCD中.
(1)如图1,点E、F分别在BC、CD上,AE、BF相交于点O,∠AOB=90°,试判断AE与BF的数量关系,并说明理由;
(2)如图2,点E、F、G、H分别在边BC、CD、DA、AB上,EG、FH相交于点O,∠GOH=90°,且EG=7,求FH的长;
(3)如图3,点E、F分别在BC、CD上,AE、BF相交于点O,∠AOB=90°,若AB=5,图中阴影部分的面积与正方形的面积之比为4:5,求△ABO的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
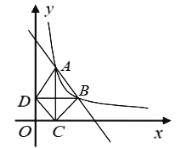
【题目】如图,在直角坐标平面内,函数![]() (x>0,m是常数)的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连结AD,DC,CB
(x>0,m是常数)的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连结AD,DC,CB
(1)若△ABD的面积为4,求点B的坐标;
(2)求证:DC∥AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一面靠墙(墙的最大可用长度为8 m)的空地上用长为24 m的篱笆围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x m,面积为S m2.
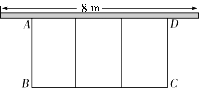
(1)求S关于x的函数关系式及自变量的取值范围;
(2)求所围成花圃的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
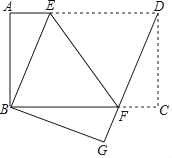
【题目】在矩形纸片ABCD中,AB=6,BC=8,现将纸片折叠,使点D与点B重合,折痕为EF,连接DF.
(1)说明△BEF是等腰三角形;
(2)求折痕EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com