
����Ŀ���ס�������ͬѧ����һ��������Ϸ:�ó���������д������![]() ��2��3�ұ�����ȫ��ͬ�Ŀ�Ƭ���������ſ�Ƭ���泯��ϴ�Ⱥ��������ȡһ�ţ�������������Ϊ
��2��3�ұ�����ȫ��ͬ�Ŀ�Ƭ���������ſ�Ƭ���泯��ϴ�Ⱥ��������ȡһ�ţ�������������Ϊ![]() ��ֵ��Ȼ��Ƭ�Żز�ϴ�ȣ����ٴ������ſ�Ƭ�������ȡһ�ţ�������������Ϊ
��ֵ��Ȼ��Ƭ�Żز�ϴ�ȣ����ٴ������ſ�Ƭ�������ȡһ�ţ�������������Ϊ![]() ��ֵ�����ν����Ϊ
��ֵ�����ν����Ϊ![]() .
.
(1)����������û���״ͼ���б��ķ�����ʾ![]() ���п��ܳ��ֵĽ��;
���п��ܳ��ֵĽ��;
(2)������¼���![]() ����ƽ��ֱ������ϵ�е�һ�㣬��
����ƽ��ֱ������ϵ�е�һ�㣬��![]() �ǵ�һ�����ڵĵ�ĸ���.
�ǵ�һ�����ڵĵ�ĸ���.
���𰸡���1�������������2��![]() .
.
��������
��1�������⻭��״ͼ���ɣ���2��![]() �ǵ�һ�����ڵĵ�ĸ��ʵ��ڵ�һ���ĵ�ĸ��������е�����ĵ�ĸ���֮��.
�ǵ�һ�����ڵĵ�ĸ��ʵ��ڵ�һ���ĵ�ĸ��������е�����ĵ�ĸ���֮��.
(1)����״ͼ�ã�
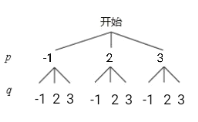
����9�ֽ����
��2���ɣ�1���ɵã�һ����9�ֽ�����ֱ�Ϊ����-1��-1������-1��2������-1��3������2��-1������2��2������2��3������3��-1������3��2������3��3�����ڵ�һ������4��.
�ࣨp��q���ڵ�һ���ĸ���P=![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
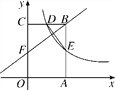
����Ŀ����ͼ������OABC�Ķ���A��C�ֱ���x���y���ϣ���B������Ϊ(2��3)��˫����y��![]() (x>0)��ͼ��BC�ϵĵ�D��AB���ڵ�E������DE����E��AB���е㣮
(x>0)��ͼ��BC�ϵĵ�D��AB���ڵ�E������DE����E��AB���е㣮
(1)���D�����ꣻ
(2)��F��OC����һ�㣬����FBC�͡�DEB���ƣ����F�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
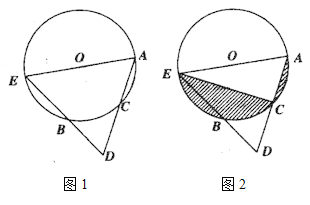
����Ŀ����ͼ1������O�У���CΪ�ӻ�AB���е㣬����AC���ӳ���D��ʹCA=CD������DB���ӳ�����O�ڵ�E������AE.
��1����֤��AE����O��ֱ����
��2����ͼ2������CE����O�İ뾶Ϊ5��AC��Ϊ4������Ӱ�������֮��.(����![]() �����) .
�����) .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD��������AEFG�У���B�ڱ�AG�ϣ���D���߶�EA���ӳ����ϣ�����BE��
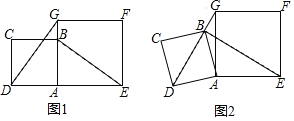
��1����ͼ1����֤��DG��BE��
��2����ͼ2����������ABCD�Ƶ�A����ʱ�뷽����ת��ʹ��Bǡ�������߶�DG�ϣ�
����֤��DG��BE��
����AB��2��AG��3�����߶�BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����ⷢ��
��ͼ1����Rt��ABC��Rt��CDE�У���ACB����DCE��90������CAB����CDE��45������Dʱ�߶�AB��һ���㣬����BE��
��գ���![]() ��ֵΪ�� ���� �ڡ�DBE�Ķ���Ϊ�� ����
��ֵΪ�� ���� �ڡ�DBE�Ķ���Ϊ�� ����

��2�����̽��
��ͼ2����Rt��ABC��Rt��CDE�У���ACB����DCE��90������CAB����CDE��60������D���߶�AB��һ���㣬����BE�����ж�![]() ��ֵ����DBE�Ķ�������˵�����ɣ�
��ֵ����DBE�Ķ�������˵�����ɣ�
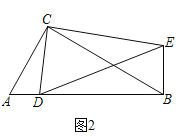
��3����չ����
��ͼ3���ڣ�2���������£�����D��Ϊֱ��AB��һ���㣬�����������䣬ȡ�߶�DE���е�M������BM��CM����AC��2������CBM��ֱ��������ʱ���߶�BE�ij��Ƕ��٣���ֱ��д���𰸣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijС����һ�鳤Ϊ16m����Ϊ9m�ľ��οյ�����������������ͬ��С·������һ���;��ε�һ��ƽ�У����������;��ε���һ��ƽ�У��յ�ʣ�µIJ�����ֲ���ݣ�ʹ�û�������ռ�����Ϊ120m2����С·�Ŀ���Ϊxm�������з��̣�
�٣�16��2x����9��x����120
��16��9��9��2x����16��2x��x��120
��16��9��9��2x��16x+x2��120��
������ȷ���ǣ�������
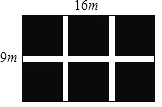
A.��B.��C.�٢�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС����9�·�������A��B���ֲ�Ʒ�����ֱ�Ϊ200����100����A��B���ֲ�Ʒ��������֮��Ϊ2��1�����ڶ��������ӣ����������A��B���ֲ�Ʒ�����������ͳ������ۣ�10�·�A��Ʒ���������������ʺ�A��Ʒ�������۵���������ȣ�B��Ʒ������������������A��Ʒ���������������ʵ�һ�룬B��Ʒ�������۵���������A��Ʒ�������۵������ʵ�2������B��Ʒ����������������Ϊx��x��0����
��1���ú���x�Ĵ���ʽ��������軯��
9�·��������� | ���������������� | 10�·��������� | |
��ƷA | 200 | �� �� | �� �� |
��ƷB | 100 | x | �� �� |
��2����9�·����ֲ�Ʒ�������۵ĺ�Ϊ90Ԫ��10�·ݸù�����������������4.4x����x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�γ�32m����ʺͳ�8m��ǽ��Χ��һ�����εIJ���
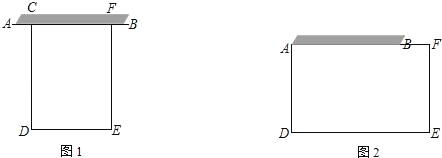
��1����ͼ1��������β���һ�߿�ǽAB�������������CDEFΧ��
����DE����xm��ֱ��д�������y��x֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
�ڲ�������ܲ��ܵ���110m2�����ܣ������ʱx��ֵ�������ܣ���˵�����ɣ�
��2����ͼ2��������β���һ����ǽAB��һ�����BF���ɣ������������ADEFΧ�ɣ������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
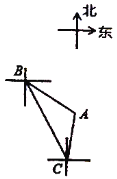
����Ŀ����ͼ���ִ���![]() ����ÿСʱ60������ٶ�����ƫ��
����ÿСʱ60������ٶ�����ƫ��![]() �������ٺ��У���
�������ٺ��У���![]() ���۲����
���۲����![]() λ����ƫ��
λ����ƫ��![]() �����ϣ��ִ�����40���ӵ���
�����ϣ��ִ�����40���ӵ���![]() ������
������![]() ���۲����
���۲����![]() λ�ڱ�ƫ��
λ�ڱ�ƫ��![]() �����ϣ���
�����ϣ���![]() �������
�������![]() �ľ���.
�ľ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com