如图所示，已知在△ABC中，∠B=2∠C，AD为BC边上的高，求证CD=AB＋BD．
|
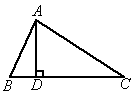
证明：在 DC上截取DE=BD，连接AE．
在△ABD和△AED中，
∴△ABD≌△AED， ∴∠AEB=∠B，AB=AE(全等三角形的对应角相等，对应边相等)． 而∠AEB=∠C＋∠EAC(三角形的一个外角等于和它不相邻的两个内角和)， 又∠AEB=∠B=2∠C(已知)， ∴∠EAC=∠C． ∴AE=EC(等角对等边)． ∴AB=EC(等量代换)． ∴CD=DE＋EC=AB＋BD． |
|
CD 和BD都在直线BC上，若BD成为CD上的一部分时，只要证明另一部分与AB相等就可以了．那么在DC上截取DE=BD，由已知条件易证△ABD≌△AED，因此有AB=CE=AB，因此此题可证． |
教材全解字词句篇系列答案科目：初中数学 来源： 题型：
19、如图所示，已知在△ABC中，D是AB的中点，E是AC上的点，且∠ABE=∠BAC，EF∥AB，DF∥BE，请猜想DF与AE有怎样的关系，并说明理由．查看答案和解析>>
科目：初中数学 来源： 题型：
如图所示，已知在Rt△ABC中，∠C=90°，BC=4，AC=4，现将△ABC沿射线CB方向平移到△A′B′C′的位置．若平移距离为3，求△ABC与△A′B′C′的重叠部分的面积．查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
19、如图所示，已知在△ABC中，∠B=90°，点D、点E分别在BC和AB上．求证：AD2+CE2=AC2+DE2．
如图所示，已知在△ABC中，AB=AC，∠BAD=β，且AD=AE，求∠EDC．（用β表示）
如图所示，已知在△ABC中，∠C=90°，AD=AC，DE⊥AB交BC于点E，若∠B=28°，则∠AEC=