
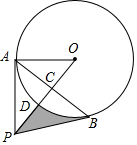
 如图,点A在⊙O上,点P是⊙O外一点,PA切⊙O于点A,连接OP交⊙O于点D,作AB⊥OP于点C,交⊙O于点B,连接PB.
如图,点A在⊙O上,点P是⊙O外一点,PA切⊙O于点A,连接OP交⊙O于点D,作AB⊥OP于点C,交⊙O于点B,连接PB.分析 (1)由PA切⊙O于点A得:∠PAO=90°,再证明△APO≌△BPO,所以∠PBO=∠PAO=90°,可得结论;
(2)①先根据垂径定理得:BC=3$\sqrt{3}$,根据勾股定理求圆的半径OB的长,利用三角函数得:∠COB=60°,利用三角形的面积公式和扇形的面积公式分别求S△OPB和S扇形DOB的值,最后利用面积差得结论;
②②分两种情况:
i)当点E在$\widehat{AFB}$上时,如图2,作辅助线,构建直角三角形和等腰直角三角形,利用同弧所对的圆周角与半径及勾股定理分别计算EH和BH的长,相加即可得BE的长;
ii)当点E在劣弧$\widehat{AB}$上时,如图3,作辅助线,同理计算EH和BH的长,最后利用勾股定理求BE的长.
解答 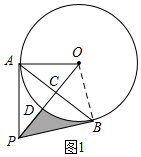 (1)证明:如图1,连接OB,
(1)证明:如图1,连接OB,
∵OP⊥AB,OP经过圆心O,
∴AC=BC,
∴OP垂直平分AB,
∴AP=BP,
∵OA=OB,OP=OP,
∴△APO≌△BPO(SSS),
∴∠PAO=∠PBO,
∵PA切⊙O于点A,
∴AP⊥OA,
∴∠PAO=90°,
∴∠PBO=∠PAO=90°,
∴OB⊥BP,
又∵点B在⊙O上,
∴PB与⊙O相切于点B;
(2)①解:如图1,∵OP⊥AB,OP经过圆心O,
∴BC=$\frac{1}{2}$AB=3$\sqrt{3}$,
∵∠PBO=∠BCO=90°,
∴∠PBC+∠OBC=∠OBC+∠BOC=90°,
∴∠PBC=∠BOC,
∴△PBC∽△BOC,
∴$\frac{BC}{OC}=\frac{PC}{BC}$
∴OC=$\frac{BC×BC}{PC}$=$\frac{3\sqrt{3}×3\sqrt{3}}{9}$=3,
∴在Rt△OCB中,OB=$\sqrt{O{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+(3\sqrt{3})^{2}}$=6,tan∠COB=$\frac{BC}{OC}$=$\sqrt{3}$,
∴∠COB=60°,
∴S△OPB=$\frac{1}{2}$×OP×BC=$\frac{1}{2}$×$(3+9)×3\sqrt{3}$=18$\sqrt{3}$,S扇DOB=$\frac{60π×{6}^{2}}{360}$=6π,
∴S阴影=S△OPB-S扇DOB=18$\sqrt{3}$-6π;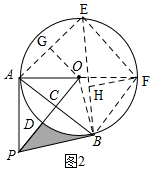
②分两种情况:
i)当点E在$\widehat{AFB}$上时,如图2,作直径AF,交⊙O于F,连接EF、EB,过O作OG⊥AE于G,过F作FH⊥EB于H,
∴EG=AG=$\frac{1}{2}$AE=$\frac{1}{2}$×$6\sqrt{2}$=3$\sqrt{2}$,
∵∠AOB=120°,OA=OB,
∴∠OAB=30°,
∴∠BEF=∠OAB=30°,
Rt△OGE中,由①知:OA=6,
∴OG=$\sqrt{O{E}^{2}-E{G}^{2}}$=$\sqrt{{6}^{2}-(3\sqrt{2})^{2}}$=3$\sqrt{2}$,
∴AG=OG,
∴△OGA是等腰直角三角形,
∴∠OAE=45°,
∴∠EBF=∠OAE=45°,
∵AF是⊙O的直径,
∴∠AEF=90°,
∴△AEF是等腰直角三角形,
∴EF=AE=6$\sqrt{2}$,
Rt△EHF中,∠BEF=30°,
∴FH=$\frac{1}{2}$EF=3$\sqrt{2}$,
∴EH=$\sqrt{E{F}^{2}-F{H}^{2}}$=$\sqrt{(6\sqrt{2})^{2}-(3\sqrt{2})^{2}}$=3$\sqrt{6}$,
Rt△BHF中,∵∠EBF=45°,
∴△BHF是等腰直角三角形,
∴BH=FH=3$\sqrt{2}$,
∴BE=3$\sqrt{2}$+3$\sqrt{6}$,
ii)当点E在劣弧$\widehat{AB}$上时,如图3,
作直径AF,并⊙O于F,连接OB、OE、BF,过B作BH⊥OE于H,
∵AF为⊙O的直径,
∴∠ABF=90°,
∵∠BAF=30°,
∴∠F=∠BOF=60°,
∵OA=OE=6,AE=6$\sqrt{2}$,
∴OA2+OE2=AE2,
∴∠AOE=90°,
∴∠EOF=90°,
∴∠EOB=30°,
Rt△OHB中,BH=$\frac{1}{2}$OB=3,
∴OH=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴EH=6-3$\sqrt{3}$,
∴BE=$\sqrt{B{H}^{2}+E{H}^{2}}$=$\sqrt{{3}^{2}+(6-3\sqrt{3})^{2}}$=$\sqrt{72-36\sqrt{3}}$=3$\sqrt{6}$-3$\sqrt{2}$;
综上所述,BE的长为3$\sqrt{6}$+3$\sqrt{2}$或3$\sqrt{6}$-3$\sqrt{2}$;
故答案为:3$\sqrt{6}$-3$\sqrt{2}$ 或3$\sqrt{6}$+3$\sqrt{2}$.
点评 本题考查了切线的性质和判定、垂径定理、三角函数、扇形的面积、三角形相似的性质和判定、圆周角定理,第2小问构建辅助线是关键,同时要采用分类讨论的思想.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
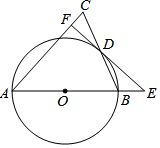 如图,在△ABC中,以AB为直径的⊙O交BC于点D,CD=BD,过点D作⊙O的切线交边AC于点F,交AB的延长线于点E.
如图,在△ABC中,以AB为直径的⊙O交BC于点D,CD=BD,过点D作⊙O的切线交边AC于点F,交AB的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{500}{x}$+$\frac{45}{x+10}$=24 | B. | $\frac{0.5}{x}$+$\frac{4.5}{x+10}$=$\frac{24}{60}$ | ||
| C. | $\frac{500}{x-10}$+$\frac{4500}{x}$=24 | D. | $\frac{0.5}{x-10}$+$\frac{4.5}{x}$=$\frac{24}{60}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
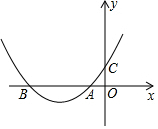 如图,抛物线y=ax2+bx+c与两坐标轴的交点分别为A、B、C,且OA=OC=1,则下列关系中正确的是( )
如图,抛物线y=ax2+bx+c与两坐标轴的交点分别为A、B、C,且OA=OC=1,则下列关系中正确的是( )| A. | a+b=-1 | B. | a-b=-1 | C. | b<2a | D. | ac<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
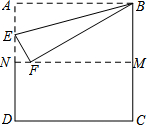 如图,把边长为2的正方形纸片ABCD先对折一次再展开,折痕为MN,然后再沿过点B的线段折叠,使得点A落在MN上的点F处,折痕交AN于点E,则NF的长为( )
如图,把边长为2的正方形纸片ABCD先对折一次再展开,折痕为MN,然后再沿过点B的线段折叠,使得点A落在MN上的点F处,折痕交AN于点E,则NF的长为( )| A. | 2 | B. | 2-$\sqrt{3}$ | C. | $\sqrt{2}$-1 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
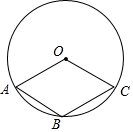 如图,点A,B,C均在圆O上,并且四边形OABC是菱形,那么∠O与2∠A的关系是( )
如图,点A,B,C均在圆O上,并且四边形OABC是菱形,那么∠O与2∠A的关系是( )| A. | ∠O>2∠A | B. | ∠O=2∠A | C. | ∠O<2∠A | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com