
【题目】直线y=kx+b与反比例函数y= ![]() (x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0) 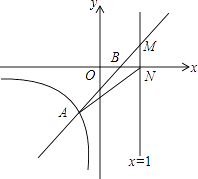
(1)求m的值;
(2)求直线AB的解析式;
(3)若直线x=t(t>1)与直线y=kx+b交于点M,与x轴交于点N,连接AN,S△AMN= ![]() ,求t的值.
,求t的值.
【答案】
(1)解:将点A(﹣1,m)代入y= ![]() ,得:m=﹣2;
,得:m=﹣2;
(2)解:由(1)知点A坐标为(﹣1,﹣2),
将点A(﹣1,﹣2)、B(1,0)代入y=kx+b,
得: ![]() ,
,
解得: ![]() ,
,
∴直线AB的解析式为:y=x﹣1;
(3)解:当x=t时,y=t﹣1,
∴点M坐标为(t,t﹣1),点N坐标为(t,0),
∵S△AMN= ![]() ,
,
∴ ![]() ×(t﹣1)(t+1)=
×(t﹣1)(t+1)= ![]() ,
,
解得:t=2或t=﹣2(舍),
∴t=2.
【解析】(1)将点A坐标代入y= ![]() 可得m的值;(2)将点A、B坐标代入y=kx+b可得关于k、b的方程,解方程求出k、b的值,可得直线解析式;(3)根据直线直线x=t与直线y=kx+b交于点M、与x轴交于点N表示出M、N的坐标,由S△AMN=
可得m的值;(2)将点A、B坐标代入y=kx+b可得关于k、b的方程,解方程求出k、b的值,可得直线解析式;(3)根据直线直线x=t与直线y=kx+b交于点M、与x轴交于点N表示出M、N的坐标,由S△AMN= ![]() 可得关于t的方程,解方程可得t的值.
可得关于t的方程,解方程可得t的值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF. 
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班13位同学参加每周一次的卫生大扫除,按学校的卫生要求需要完成总面积为60m2的三个项目的任务,三个项目的面积比例和每人每分钟完成各所示:项目的工作量如图: 
(1)从统计图中可知:擦玻璃的面积占总面积的百分比为 , 每人每分钟擦课桌椅m2;
(2)扫地拖地的面积是m2;
(3)他们一起完成扫地和拖地任务后,把这13人分成两组,一组去擦玻璃,一组去擦课桌椅,如果你是卫生委员,该如何分配这两组的人数,才能最快地完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,DG平分∠ADB交AB于点G,GF⊥BD于F. 
(1)求证:△ADG≌△FDG;
(2)若BG=2AG,BD=2 ![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中弧FK1 , 弧K1K2 , 弧K2K3 , 弧K3K4 , 弧K4K5 , 弧K5K6 , …的圆心依次按点A,B,C,D,E,F循环,其弧长分别记为L1 , L2 , L3 , L4 , L5 , L6 , ….当AB=1时,L2016等于( ) 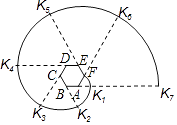
A.![]()
B.![]()
C.![]()
D.![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙﹣我最喜爱的长沙小吃”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图: 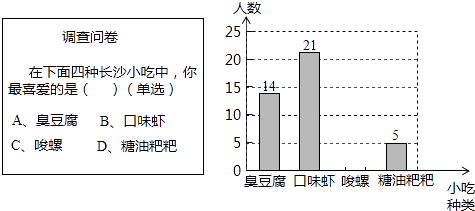
请根据所给信息解答以下问题:
(1)请补全条形统计图;
(2)若全校有2000名同学,请估计全校同学中最喜爱“臭豆腐”的同学有多少人?
(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=6cm,AD=9cm,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=4 ![]() cm,则EF+CF的长为cm.
cm,则EF+CF的长为cm. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com