练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．对于二次函数 y=（x-1）2+2 的图象，下列说法正确的是（　　）
    A．开口向下B．顶点坐标是（-1，2）C．对称轴是x=1D．与x轴有两个交点

    分析 由抛物线解析式可求得其开口方向、顶点坐标、对称轴，再结合一元二次方程与函数图象与x轴的交点的关系可求得答案．

    解答 解：
    ∵y=（x-1）2+2，
    ∴抛物线开口向上，顶点坐标为（1，2），对称轴为x=1，
    令y=0可得（x-1）2+2=0，该方程无实数根，
    ∴抛物线与x轴没有交点，
    故选C．

    点评 本题主要考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在y=a（x-h）2+k中，顶点坐标为（h，k），对称轴为x=h．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．当x为多少时，$\sqrt{{x}^{2}+4}$+$\sqrt{{x}^{2}-6x+25}$取得最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

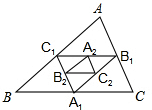    1．如图，在△ABC中，A1、B1、C1分别是BC、CA、AB的中点，A2、B2、C2分别是B1C1、C1A1、A1B1的中点，…，An、Bn、Cn分别是Bn-1Cn-1、Cn-1An-1、An-1Bn-1的中点，假设△ABC的周长为a，则△A1B1C1的周长为$\frac{1}{2}$a，△A2B2C2的周长为$\frac{1}{4}$a，…，△AnBnCn的周长为$\frac{1}{{2}^{n}}$a．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列说法错误的是（　　）
    A．正整数和正分数统称正有理数B．两个无理数相乘的结果可能等于零
    C．正整数，0，负整数统称为整数D．3.1415926是小数，也是分数

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

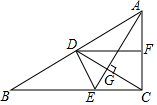    5．如图，在△ABC中，∠ACB=90°，AE平分∠BAC，CD⊥AE交AE于点G，交AB于点D，DF∥BE交AC于点F．求证：DC平分∠FDE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列解方程的各种变形中，正确的是（　　）
    A．由5x=4x+1可得4x-5x=1B．由3（x-1）-2（2x-3）=1可得3x-3-4x-6=1
    C．由$\frac{x+2}{4}$-1=$\frac{2x-3}{6}$可得3（x+2）-1=2（2x-3）D．由$\frac{1}{2}$x=$\frac{1}{4}$可得x=$\frac{1}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，在Rt△ABC中，∠BAC=90°，AD是中线，AE是高，AC=6，AD=5，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

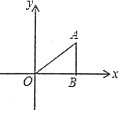    19．如图．在△ABO中，AB丄OB，OB=$\sqrt{3}$，AB=1，将△ABO绕O点逆时计旋转90°后得到△A1B1O，则点A1的坐标为（　　）
    A．（-1，$\sqrt{3}$）B．（-1，$\sqrt{3}$）或（1，-$\sqrt{3}$）C．（-1，-$\sqrt{3}$）D．（-1，-$\sqrt{3}$）或（-$\sqrt{3}$，-1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

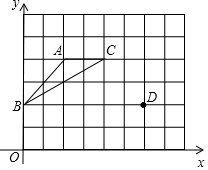    20．如图，在坐标系的第一象限建立网格，网格中的每个小正方形边长都为1，格点△ABC的顶点坐标分别为A（2，4）、B（0，2）、C（4，4）．
    （1）若△ABC外接圆的圆心为P，则点P的坐标为（3，1）．
    （2）以点D为顶点，在网格中画一个格点△DEF，使△DEF∽△ABC，且相似比为1：2．（画出符合要求的一个三角形即可）

    查看答案和解析>>

    同步练习册答案