
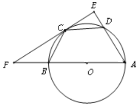
【题目】如图,AB是⊙O的直径,C,D在⊙O上,且BC=CD,过C作CE⊥AD,交AD延长线于E,交AB延长线于F点,
(1)求证:EF是⊙O的切线;
(2)若AB=4ED,求cos∠ABC的值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)要证EF是⊙O的切线,只要证∠OCE=90°,根据OC=OA得到∠OCA=∠OAC,再证∠OCA=∠EAC,从而证∠OCA+∠ECA=90°;
(3)先证△CDE∽△ABC得到对应边成比例,由AB=4DE,BC=CD得到BC=![]() AB,从而求出cos∠ABC=
AB,从而求出cos∠ABC=![]() .
.
(1)证明:连接OC、AC
∵CE⊥AD
∴∠EAC+∠ECA=90°
∵OC=OA
∴∠OCA=∠OAC
又∵BC=CD
∴∠OAC=∠EAC
∴∠OCA=∠EAC
∴∠ECA+∠OCA=90°
∴EF是⊙O的切线.
(2)解:∵EF是⊙O的切线
∴∠ECD=∠EAC
又∵BC=CD
∴∠EAC=∠BAC
∴∠ECD=∠BAC
又∵AB是直径
∴∠BCA=90°
在△BAC和△DCE中
∠BCA=∠DEC=90°
∠ECD=∠CAB
∴△CDE∽△ABC
∴![]()
又∵AB=4DE,CD=BC
∴![]()
![]()
![]() .
.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】已知:在以![]() 为原点的平面直角坐标系中,抛物线的顶点为
为原点的平面直角坐标系中,抛物线的顶点为![]() 点,且经过点
点,且经过点![]() ,
,![]() ,
,![]() 三点.
三点.
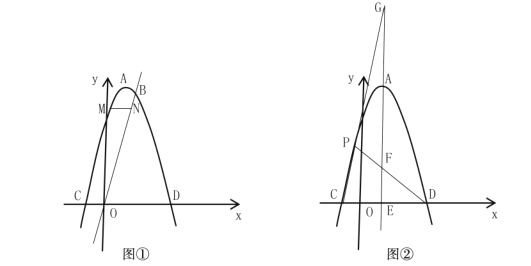
(1)求直线![]() 和该抛物线相应的函数表达式;
和该抛物线相应的函数表达式;
(2)如图①,点![]() 为抛物线上的一个动点,且在直线
为抛物线上的一个动点,且在直线![]() 的上方,过点
的上方,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() ,求
,求![]() 的最大值.
的最大值.
(3)如图②,过点![]() 的直线交
的直线交![]() 轴于点
轴于点![]() ,且
,且![]() 轴,点
轴,点![]() 是抛物线上
是抛物线上![]() ,
,![]() 之间的一个动点,直线
之间的一个动点,直线![]() ,
,![]() 与
与![]() 分别交于
分别交于![]() ,
,![]() ,当点
,当点![]() 运动时,
运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
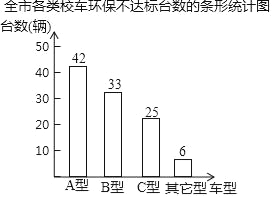
【题目】长春市对全市各类(A型、B型、C型.其它型)校车共848辆进行环保达标普查,普查结果绘制成如下条形统计图:
(1)求全市各类环保不达标校车的总数;
(2)求全市848辆校车中环保不达标校车的百分比;
(3)规定环保不达标校车必须进行维修,费用为:A型500元/辆,B型1000元/辆,C型600元/辆,其它型300元/辆,求全市需要进行维修的环保不达标校车维修费的总和;
(4)若每辆校车乘坐40名学生,那么一次性维修全部不达标校车将会影响全市80000名学生乘校车上学的百分比是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(2k﹣1)x+k2+k﹣1=0有实数根.
(1)求k的取值范围;
(2)若此方程的两实数根x1,x2满足x12+x22=11,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在反比例函数y= ![]() 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= ![]() 的图象上运动,若tan∠CAB=2,则k的值为( )
的图象上运动,若tan∠CAB=2,则k的值为( )
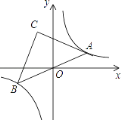
A. ﹣3 B. ﹣6 C. ﹣9 D. ﹣12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选择:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其他),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):

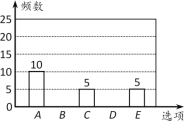
根据以上信息解答下列问题:
⑴ 这次被调查的学生有多少人?
⑵ 表中m的值为 ,并补全条形统计图;
⑶若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调查结果,就中学生如何合理使用手机给出你的一条建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
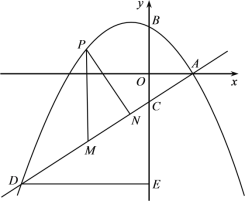
【题目】如图,抛物线![]() 与
与![]() 轴交于点A(2,0),交
轴交于点A(2,0),交![]() 轴于点B(0,
轴于点B(0,![]() ),直线
),直线![]() 过点A与y轴交于点C,与抛物线的另一个交点为D,作DE⊥y轴于点E.设点P是直线AD上方的抛物线上一动点(不与点A、D重合),过点P作y轴的平行线,交直线AD于点M,作PN⊥AD于点N.
过点A与y轴交于点C,与抛物线的另一个交点为D,作DE⊥y轴于点E.设点P是直线AD上方的抛物线上一动点(不与点A、D重合),过点P作y轴的平行线,交直线AD于点M,作PN⊥AD于点N.
⑴填空:![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
⑵探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由;
⑶设△PMN的周长为![]() ,点P的横坐标为x,求
,点P的横坐标为x,求![]() 与x的函数关系式,并求出
与x的函数关系式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
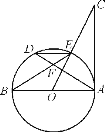
【题目】如图,AB是⊙O的直径,AD是弦,OC垂直AD于F交⊙O于E,连结DE,BE,且∠C=∠BED.
(1)求证:AC是⊙O的切线;
(2)若OA=10,AD=16,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com