
【题目】如图,△ABC在直角坐标系中,
(1)写出△ABC各点的坐标.A( , )B( , )C( , ).
(2)若把△ABC向上平移1个单位,再向右平移3个单位得△A′B′C′,在图中画出△A′B′C′,并写出A′、B′、C′的坐标.A′( , )B′( , )C′( , ).
(3)连结CA′,CB′,则△CA′B′的面积是 .
【答案】
(1)﹣1;﹣1;4;2;1;3
(2)2;0;7;3;4;4
(3)5
【解析】解:(1)由图形可知△ABC各点的坐标如下:A(﹣1,﹣1)、B(4,2)、C(1,3),
所以答案是:﹣1、﹣1、4、2、1、3;
⑵平移后△A′B′C′如图所示,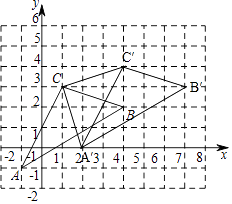
则A′(2,0)、B′(7,3)、C′(4,4),
所以答案是:2、0、7、3、4、4;
⑶△CA′B′的面积是3×4﹣ ![]() ×1×3﹣
×1×3﹣ ![]() ×2×4﹣
×2×4﹣ ![]() ×1×3=5,
×1×3=5,
所以答案是:5.
【考点精析】本题主要考查了坐标与图形变化-平移的相关知识点,需要掌握新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等才能正确解答此题.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,b满足![]() +(c-7)2=0.
+(c-7)2=0.
(1) a= ,b= ,c= .
(2) 若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= .(用含t的代数式表示)
(4) 请问:3BC-2AB的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠BAD=60°
(1)如图1,点E为线段AB的中点,连接DE、CE,若AB=4,求线段EC的长;
(2)如图2,M为线段AC上一点(不与A、C重合),以AM为边向上构造等边三角形AMN,连接NC、DM,Q为线段NC的中点,连接DQ、MQ,判断DM与DQ的数量关系,并证明你的结论.
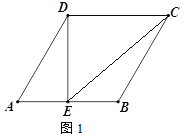
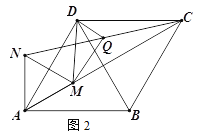
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据生物学研究结果,青春期男女生身高增长速度呈现如下图规律,由图可以判断,下列说法错误的是( ) 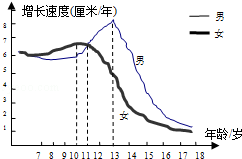
A.男生在13岁时身高增长速度最快
B.女生在10岁以后身高增长速度放慢
C.11岁时男女生身高增长速度基本相同
D.女生身高增长的速度总比男生慢
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,完成下列推理,并填写理由,如图,∠B=∠D,∠1=∠2,求证:AB∥CD. 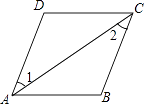
【证明】∵∠1=∠2(已知),
∴∥()
∴∠DAB+∠=180°()
∵∠B=∠D(已知)
∴∠DAB+∠=180°()
∴AB∥CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上有A、B两点,所表示的数分别为n,n+6,A点以每秒5个单位长度的速度向右运动,同时B点以每秒3个单位长度的速度也向右运动,设运动时间为t 秒.
(1)当n=1时,求AB的值;
(2)当t 为何值时,A、B两点重合;
(3)在上述运动的过程中,若P为线段AB的中点,数轴上点C所表示的数为n+10是否存在t 的值,使得线段PC=4,若存在,求t 的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
(1)在“十一”期间,小明等同学随家长共15人到游乐园游玩,成人门票每张50元,学生门票是6折优惠.他们购票共花了650元,求一共去了几个家长、几个学生?
(2)甲、乙两人骑自行车同时从相距65千米的两地出发相向而行,甲的速度是每小时17.5千米,乙的速度是每小时15千米,求经过几小时甲、乙两人相距32.5千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)小白同学在研究有理数分类时,认为“所有的无限循环小数都可以化为分数”,例如,![]() 怎样化成分数?
怎样化成分数?
小白的思路是这样的:
设![]() =x,则10×
=x,则10×![]() =10x即
=10x即![]() =10x,
=10x,![]() ﹣
﹣![]() =10x﹣x,3=9x,x=
=10x﹣x,3=9x,x=![]()
(解决问题)请你按照小白的思路解决下列问题:
(1)将![]() 化成分数;
化成分数;
(2)将![]() 化成分数.
化成分数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com