
【题目】如图,在△ABC中,∠C=90°,AC=BC,BD平分∠CBA交AC于点D,DE⊥AB于点E,且△DEA的周长为2019cm,则AB=______.
 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 为直线
为直线![]() 上的一个动点(与点
上的一个动点(与点![]() 不重合),分别作
不重合),分别作![]() 和
和![]() 的角平分线,两角平分线所在直线交于点
的角平分线,两角平分线所在直线交于点![]() .
.
(1)若点![]() 在线段
在线段![]() 上,如图1.
上,如图1.
①依题意补全图1;
②求![]() 的度数;
的度数;
(2)当点![]() 在直线
在直线![]() 上运动时,
上运动时,![]() 的度数是否变化?若不变,请说明理由;若变化,画出相应的图形,并直接写出
的度数是否变化?若不变,请说明理由;若变化,画出相应的图形,并直接写出![]() 的度数.
的度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小学学生较多,为了便于学生尽快就餐,师生约定:早餐一人一份,一份两样,一样一个,食堂师傅在窗口随机发放(发放的食品价格一样),食堂在某天早餐提供了猪肉包、面包、鸡蛋、油饼四样食品.
(1)按约定,“小李同学在该天早餐得到两个油饼”是 事件;(可能,必然,不可能)
(2)请用列表或树状图的方法,求出小张同学该天早餐刚好得到猪肉包和油饼的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批甲、乙两种办公桌若干张,并且每买1张办公桌必须买2把椅子,椅子每把100元,若学校购进20张甲种办公桌和15张乙种办公桌共花费24000元;购买10张甲种办公桌比购买5张乙种办公桌多花费2000元.
(1)求甲、乙两种办公桌每张各多少元?
(2)若学校购买甲乙两种办公桌共40张,且甲种办公桌数量不多于乙种办公桌数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1 m长的影子如图所示,已知窗框的影子DE的点E到窗下墙脚的距离CE=3.9 m,窗口底边离地面的距离BC=1.2 m,试求窗口的高度(即AB的值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,如果BD,CE分别是∠ABC,∠ACB的平分线且他们相交于点P,设∠A=n°.

(1)求∠BPC的度数(用含n的代数式表示),写出推理过程.
(2)当∠BPC=125°时,∠A= .
(3)当n=60°时,EB=7,BC=12,DC的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:四边形ABCD中,∠ABC=∠ADC=90°,AB=BC,连接BD.
(1)画出示意图;
(2)请问:DB平分∠ADC吗?请给出结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
问题:如图1,点A,B在直线l的同侧,在直线l上找一点P,使得AP+BP的值最小.
小明的思路是:如图2所示,先作点A关于直线l的对称点A′,使点A′,B分别位于直线l的两侧,再连接A′B,根据“两点之间线段最短”可知A′B与直线l的交点P即为所求.
请你参考小明同学的思路,探究并解决下列问题:
(1)如图3,在图2的基础上,设AA'与直线l的交点为C,过点B作BD⊥l,垂足为D.若CP=1,AC=1,PD=2,直接写出AP+BP的值;
(2)将(1)中的条件“AC=1”去掉,换成“BD=4﹣AC”,其它条件不变,直接写出此时AP+BP的值;
(3)请结合图形,求![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题背景】
(1)如图1的图形我们把它称为“8字形”,请说明![]() ;
;

【简单应用】
(2)阅读下面的内容,并解决后面的问题:如图2, AP、CP分别平分∠BAD. ∠BCD,若∠ABC=36°,∠ADC=16°,求∠P的度数;

解:∵AP、CP分别平分∠BAD. ∠BCD
∴∠1=∠2,∠3=∠4
由(1)的结论得: ![]()
①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D
∴∠P =![]() (∠B+∠D)=26°.
(∠B+∠D)=26°.
【问题探究】如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,请猜想![]() 的度数,并说明理由.
的度数,并说明理由.

【拓展延伸】
① 在图4中,若设∠C=α,∠B=β,∠CAP=![]() ∠CAB,∠CDP=
∠CAB,∠CDP=![]() ∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),
∠CDB,试问∠P与∠C、∠B之间的数量关系为:________________(用α、β表示∠P),

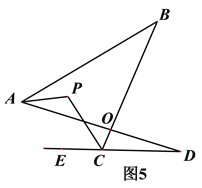
②在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论______________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com