
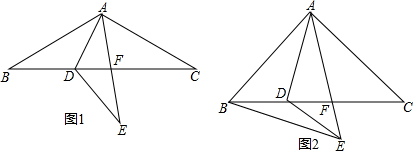
分析 ①根据翻折变换的性质得到∠ADB=∠ADE,根据邻补角的概念计算即可;
②设∠EDC=∠DAB=x,用x表示出∠ADB和∠ADE,根据翻折变换的性质列出方程,解方程得到答案;
③作CH⊥AE于H,根据等腰直角三角形的性质求出AB、AC的长,根据直角三角形的性质求出CH的长,根据三角形面积公式计算即可.
解答 解:①∵∠ADB=112°,
∴∠ADE=112°,∠ADC=180°-112°=68°,
∴∠EDC=∠ADE-∠ADC=44°,
故答案为:44°;
②设∠EDC=∠DAB=x,
则∠ADB=180°-45°-x,
∠ADE=45°+x+x,
∴180°-45°-x=45°+x+x,
解得,x=30°,
∵∠EDC=30°,DB=DE,
∴∠DBE=15°,
∴∠ABE=60°,又AB=AE, ∴△ABE是等边三角形;
∴△ABE是等边三角形;
③作CH⊥AE于H,
∵∠BAC=90°,AB=AC,BC=4,
∴AB=AC=2$\sqrt{2}$,
∵∠EAC=90°-60°=30°,
∴CH=$\frac{1}{2}$AC=$\sqrt{2}$,
∴△ACE的面积=$\frac{1}{2}$×AE×CH=2.
点评 本题考查的是翻折变换的性质和等边三角形的判定以及三角形的内角和定理、三角形的外角的性质,找准翻折变换中对应边、对应角是解题的关键,注意相关定理、性质的灵活运用.


科目:初中数学 来源: 题型:选择题
| A. | y=4x2-8x-7 | B. | y=4x2-8x+1 | C. | y=2x2-4x+1 | D. | y=-2x2-4x+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
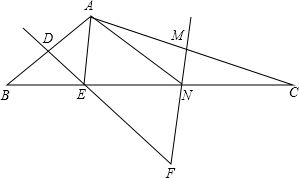 如图,在纸片△ABC中,点D、E、M、N都在边上,现将∠B,∠C分别沿MN折叠,使得点B、C与点A恰好重合,DE和MN交于点F.
如图,在纸片△ABC中,点D、E、M、N都在边上,现将∠B,∠C分别沿MN折叠,使得点B、C与点A恰好重合,DE和MN交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com