
����Ŀ������̽��
��![]() ����ͼ�٣���֪������
����ͼ�٣���֪������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ����
����![]() ��
��![]() �ֱ��DZ�
�ֱ��DZ�![]() ��
��![]() �����㣬��
�����㣬��![]() ������
������![]() ��
��![]() �����ڵ�
�����ڵ�![]() ������
������![]() ��
��![]() ��λ�ù�ϵ����֤����Ľ��ۣ�
��λ�ù�ϵ����֤����Ľ��ۣ�
��![]() ����ͼ�ڣ���֪������
����ͼ�ڣ���֪������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ����
����![]() ��
��![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ��
��![]() ͬʱ����������ͬ���ٶ���
ͬʱ����������ͬ���ٶ���![]() ��
��![]() �������յ�
�������յ�![]() ��
��![]() �˶�������
�˶�������![]() ��
��![]() �����ڵ�
�����ڵ�![]() ����
����![]() �ܳ������ֵ��
�ܳ������ֵ��
������
��![]() ����ͼ����
����ͼ����![]() Ϊ�߳�Ϊ
Ϊ�߳�Ϊ![]() ������
������![]() �ĶԽ��ߣ�
�ĶԽ��ߣ� ![]() ����
����![]() ��
��![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ��
��![]() ͬʱ����������ͬ���ٶ���
ͬʱ����������ͬ���ٶ���![]() ��
��![]() ���յ�
���յ�![]() ��
��![]() �˶�������
�˶�������![]() ��
��![]() �����ڵ�
�����ڵ�![]() ����
����![]() �ܳ������ֵ��
�ܳ������ֵ��



���𰸡���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
�������������������1�����ۣ�AM��BN��ֻҪ֤����ABM�ա�BCN���ɽ�����⣻
��2����ͼ���У���ABΪб������������ֱ����������AEB����AEB=90������EF��PA��E����EG��PB��G������EP������֤��PA+PB=2EF�����EF�����ֵ���ɽ�����⣻
��3����ͼ���У��ӳ�DA��K��ʹ��AK=AB������ABK�ǵȱ������Σ�����PK��ȡPH=PB������֤��PA+PB=PK�����PK�����ֵ���ɽ�����⣻
����������⣺��1�����ۣ�AM��BN������������
��ͼ���У����ı���ABCD�������Σ���AB=BC����ABM=��BCN=90������BM=CN�����ABM�ա�BCN�����BAM=��CBN���ߡ�CBN+��ABN=90�������ABN+��BAM=90�������APB=90������AM��BN��
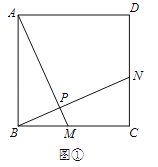
��2����ͼ���У���ABΪб������������ֱ����������AEB����AEB=90������EF��PA��E����EG��PB��G������EP��
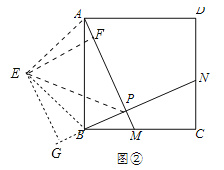
�ߡ�EFP=��FPG=��G=90�������ı���EFPG�Ǿ��Σ����FEG=��AEB=90�������AEF=��BEG����EA=EB����EFA=��G=90�������AEF�ա�BEG����EF=EG��AF=BG�����ı���EFPG�������Σ���PA+PB=PF+AF+PG��BG=2PF=2EF����EF��AE����EF�����ֵ=AE=![]() �����APB�ܳ������ֵ=
�����APB�ܳ������ֵ=![]() ��
��
��3����ͼ���У��ӳ�DA��K��ʹ��AK=AB������ABK�ǵȱ������Σ�����PK��ȡPH=PB��
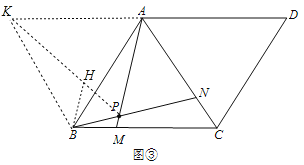
��AB=BC����ABM=��BCN��BM=CN�����ABM�ա�BCN�����BAM=��CBN�����APN=��BAM+��ABP=��CBN+��ABN=60�������APB=120�����ߡ�AKB=60�������AKB+��APB=180������A��K��B��P�ĵ㹲Բ�����BPH=��KAB=60������PH=PB�����PBH�ǵȱ������Σ����KBA=��HBP��BH=BP�����KBH=��ABP����BK=BA�����KBH�ա�ABP����HK=AP����PA+PB=KH+PH=PK����PK��ֵ���ʱ����APB���ܳ��������PK����ABK���Բ��ֱ��ʱ��PK��ֵ������ֵΪ4�����PAB���ܳ����ֵ=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�ǵȱ������Σ���P�ڡ�ABC�ڣ���Q�ڡ�ABC�⣬�ֱ�����AP��BP��AQ��CQ����ABP=��ACQ, BP=CQ.
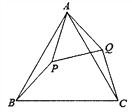
(1)��֤����ABP�ա�ACQ��
(2)����PQ,��֤��APQ�ǵȱ������Σ�
(3)����P���CPQ����![]() PQCΪ���ǵĵ��������Σ��ҡ�BPC=100
PQCΪ���ǵĵ��������Σ��ҡ�BPC=100![]() �����APB�Ķ���.
�����APB�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,A(-1��5)��B��-1��0����C��-4��3��.
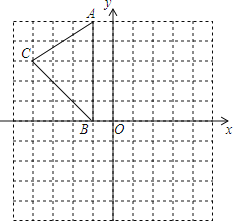
��1����ͼ��������ABC����y��ĶԳ�ͼ����A1B1C1��
��2��д����A1��B1��C1�����ꣻ
��3����y���ϻ�����P��ʹPA+PC��С��
��4����������AA1C1B1BC�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���BAC��90����AB��AC����DΪBC���е㣬ֱ�ǡ�MDN�Ƶ�D��ת��DM��DN�ֱ����AB��AC����E��F���㣬���н��ۣ��١�DEF�ǵ���ֱ�������Σ���AE��CF���ۡ�BDE�ա�ADF����BE��CF��EF��������ȷ�������� ��
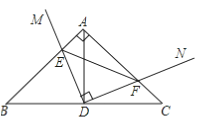
A. �٢ڢ� B. �ڢۢ�
C. �٢ڢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����Ƥ�����α�Ե��������״��MN=4�������߶��㴦����MN�ľ�����4��Ҫ����Ƥ�Ͻ���һ����ABCD��ʹ���ζ���B��C���ڱ�MN�ϣ�A��D�����������ϣ�
��1����ͼ�����ʵ�������ϵ���������߽���ʽ��
��2�������ABCD���ܳ�ΪL����C������Ϊ��m��0������L��m�Ĺ�ϵʽ����Ҫ��д�Ա���ȡֵ��Χ����
��3������������ȥ�ľ�����Ƥ���ܳ��ܷ����9.5����������9.5����˵�����ɣ�������9.5��������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������![]() �۵��ķ����У���һ�����ж�ֽ����������
�۵��ķ����У���һ�����ж�ֽ����������![]() ��
�� ![]() ����ƽ�е��ǣ� ����
����ƽ�е��ǣ� ����

A. ��ͼ![]() ��չ������
��չ������![]()
B. ��ͼ![]() ��չ������
��չ������![]()
C. ��ͼ![]() �����
�����![]()
D. ��ͼ![]() ��չ��������
��չ��������![]() �۵��������ۺ۵Ľ���Ϊ
�۵��������ۺ۵Ľ���Ϊ![]() �����
�����![]() ��
�� ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
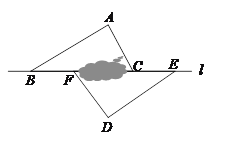
����Ŀ����ͼ����B��F��C��E��ֱ��l��(F��C֮�䲻��ֱ�Ӳ���)����A��D��l��࣬���AB��DE��AB��DE����A����D��
(1)��֤����ABC�ա�DEF��
(2)��BE=10m��BF=3m����FC�ij�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�ֳ�������飬�������ȣ��ı�ͬ���������һ���һ�������壬���Ϊ216�������ף����Ȿ��ĸ߶ȣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com