已知:圆O的半径长为5,弦AB与弦CD平行,AB=6,CD=8.求弦AB与弦CD之间的距离.
【答案】
分析:分两种情况考虑:(i)当两条弦在圆心O异侧时,如图1所示:过O作OE⊥AB,交CD于F点,连接OB,OD,可得出OB=OD=5,在直角三角形OBE和直角三角形ODF中,利用勾股定理分别求出OE与OF,用OE-OF求出EF,即为两弦间的距离;(ii)如图2所示,同理求出OE与OF的长,用OE-OF求出EF,即为两弦间的距离,综上,得到所有满足题意的两弦的距离.
解答:
解:分两种情况:
(i)当两条弦在圆心O异侧时,如图1所示:
过O作OE⊥AB,交CD于F点,
连接OB,OD,可得出OB=OD=5,
∵AB∥CD,∴EF⊥CD,
∴E为AB中点,F为CD中点,
又∵AB=6,CD=8,
∴EB=3,FD=4,
在Rt△OEB和Rt△ODF中,
利用勾股定理得:OE=
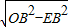
=4,OF=

=3,
则弦AB与CD间的距离EF=OE+OF=4+3=7;
(ii)当两条弦在圆心O同侧时,如图2所示:
同理求出OE=4,OF=3,
则弦AB与CD间的距离EF=OE-OF=4-3=1.
综上,弦AB与CD间的距离为1或7.
点评:此题考查了垂径定理,以及勾股定理,利用了分类讨论的思想,熟练掌握定理是解本题的关键.


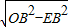 =4,OF=
=4,OF= =3,
=3,

