
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 由
由![]() 绕点
绕点![]() 顺时针旋转得到,其中点
顺时针旋转得到,其中点![]() 与点
与点![]() 、点
、点![]() 与点
与点![]() 是对应点,连接
是对应点,连接![]() ,且
,且![]() 、
、![]() 、
、![]() 在同一条直线上,则
在同一条直线上,则![]() 的长为( )
的长为( )

A. 3 B. ![]() C. 4 D.
C. 4 D. ![]()
【答案】A
【解析】
先利用互余计算出∠BAC=30°,再根据含30度的直角三角形三边的关系得到AB=2BC=2,接着根据旋转的性质得A′B′=AB=2,B′C=BC=1,A′C=AC,∠A′=∠BAC=30°,∠A′B′C=∠B=60°,于是可判断△CAA′为等腰三角形,所以∠CAA′=∠A′=30°,再利用三角形外角性质计算出∠B′CA=30°,可得B′A=B′C=1,然后利用AA′=AB′+A′B′进行计算.
∵∠ACB=90°,∠B=60°,
∴∠BAC=30°,
∴AB=2BC=2×1=2,
∵△ABC绕点C顺时针旋转得到△A′B′C′,
∴A′B′=AB=2,B′C=BC=1,A′C=AC,∠A′=∠BAC=30°,∠A′B′C=∠B=60°,
∴△CAA′为等腰三角形,
∴∠CAA′=∠A′=30°,
∵A、B′、A′在同一条直线上,
∴∠A′B′C=∠B′AC+∠B′CA,
∴∠B′CA=60°-30°=30°,
∴B′A=B′C=1,
∴AA′=AB′+A′B′=2+1=3.
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,点![]() 为平面直角坐标系的原点,在矩形
为平面直角坐标系的原点,在矩形![]() 中,两边
中,两边![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,且点
轴上,且点![]() 满足:
满足:![]() .
.


(1)求点![]() 的坐标(___,_____);
的坐标(___,_____);
(2)若过点![]() 的直线
的直线![]() 与矩形
与矩形![]() 的
的![]() 边交于点
边交于点![]() ,且将矩形
,且将矩形![]() 的面积分为
的面积分为![]() 两部分,
两部分,
①求直线![]() 的解析式;
的解析式;
②在直线![]() 确定一点
确定一点![]() ,使得
,使得![]() 的面积等于矩形
的面积等于矩形![]() 的面积,求点
的面积,求点![]() 的坐标;
的坐标;
(3)![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() 在坐标轴上,
在坐标轴上,![]() 为(2)中直线
为(2)中直线![]() 上一动点,若四点
上一动点,若四点![]() 、
、![]() 、
、![]() 、
、![]() 构成平行四边形,直接写出
构成平行四边形,直接写出![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某山是某市民周末休闲爬山的好去处,但总有些市民随手丢垃圾的情况出现.为了美化环境,提高市民的环保意识,某外国语学校某附属学校青年志愿者协会组织50人的青年志愿者团队,在周末前往临某森林公园捡垃圾.已知平均每分钟男生可以捡3件垃圾,女生可以捡2件垃圾,且该团队平均每分钟可以捡130件垃圾.请问该团队的男生和女生各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点G、H分别是BC、CD边上的点,直线GH与AB、AD的延长线相交于点E、F,连接AG、AH.
(1)当BG=2,DH=3时,则GH:HF= ,∠AGH= °;
(2)若BG=3,DH=1,求DF、EG的长;
(3)设BG=x,DH=y,若△ABG∽△FDH,求y与x之间的函数关系式,并求出y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆E是三角形ABC的外接圆, ∠BAC=45°,AO⊥BC于O,且BO=2,CO=3,分别以BC、AO所在直线建立x轴.
(1)求三角形ABC的外接圆直径;
(2)求过ABC三点的抛物线的解析式;
(3)设P是(2)中抛物线上的一个动点,且三角形AOP为直角三角形,则这样的点P有几个?(只需写出个数,无需解答过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | 200﹣2x |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.
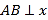
查看答案和解析>>
科目:初中数学 来源: 题型:
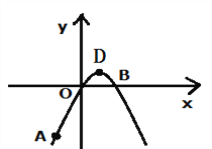
【题目】如图:在平面直角坐标系中,抛物线![]() 经过A(—2,—4 ),O(0,0),B(2,0)三点.
经过A(—2,—4 ),O(0,0),B(2,0)三点.
(1)求抛物线![]() 的解析式和顶点坐标D.
的解析式和顶点坐标D.
(2)若使![]() 轴上一点P,使P 到A、D的距离之和最小,求P的坐标.
轴上一点P,使P 到A、D的距离之和最小,求P的坐标.
(3)若抛物线对称轴上一点M,使AM + OM最小,求AM + OM的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com