
| 4 | 6 | 8 | 10 | … | 2n | … |
| 3 | 8 | 15 | 24 | … | … | |
| 5 | 10 | 17 | 26 | … | … |
分析 (1)观察表格,即可求解;
(2)观察表中每列三个数,可知它们都是一组勾股数;
(3)利用勾股定理即可求解;
解答 解:(1)由图表可以得出:
∵n=2时,4=2×2,3=22-1,5=22+1,
n=3时,6=2×3,8=32-1,10=32+1,
n=4时,8=2×4,15=42-1,17=42+1,
n=5时,10=2×5,24=52-1,26=52+1,
∴n=n时,2n,n2-1,n2+1.
填表如下:
| 4 | 6 | 8 | 10 | … | 2n | … |
| 3 | 8 | 15 | 24 | … | n2-1 | … |
| 5 | 10 | 17 | 26 | … | n2+1 | … |
点评 本题考查了勾股数:满足a2+b2=c2 的三个正整数,称为勾股数.解题的关键是仔细观察表中的数据,找出规律,进而利用规律解决问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 如图,O为Rt△ABC的直角边AC上一点,以OC为半径的半圆与斜边AB相切于点D,交AC于点E,已知AB=5,AC=4,求BD的长和⊙O的半径.
如图,O为Rt△ABC的直角边AC上一点,以OC为半径的半圆与斜边AB相切于点D,交AC于点E,已知AB=5,AC=4,求BD的长和⊙O的半径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
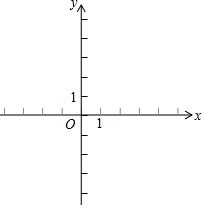 在平面直角坐标系xOy中,对于点P和⊙O给出如下定义:若⊙O上存在两个点A、B,使得∠APB=60°,则称P为⊙O的关联点.
在平面直角坐标系xOy中,对于点P和⊙O给出如下定义:若⊙O上存在两个点A、B,使得∠APB=60°,则称P为⊙O的关联点.查看答案和解析>>
科目:初中数学 来源:2017届江苏省无锡市九年级下学期第一次模拟考试数学试卷(解析版) 题型:解答题
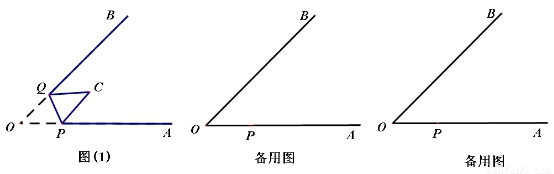
如图(1),∠AOB=45°,点P、Q分别是边OA,OB上的两点,且OP=2cm.将∠O沿PQ折叠,点O落在平面内点C处.
(1)①当PC∥QB时,OQ= ;
②当PC⊥QB时,求OQ的长.
(2)当折叠后重叠部分为等腰三角形时,求OQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com