
分析 (1)证明△ADB≌△CDE(SAS),得:∠BAD=∠ACB=40°,则∠BAC=80°;
(2)作辅助线,构建全等三角形,先利用△EFH≌△BFN(AAS),得:BN=EH,再证明BN=BM,继续证明△DEH≌△DBM,证明∠AMD=90°,所以∠AHD=90°,根据等腰三角形三线合一可得结论.
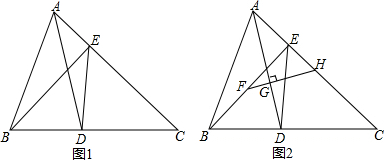
解答 解:(1)如图1,∵AD=DC,∠ACB=40°,
∴∠DAC=∠ACB=40°,
∴∠ADB=∠C+∠DAC=80°,
在△ADB和△CDE中,
∵$\left\{\begin{array}{l}{AD=DC}\\{∠ADB=∠EDC}\\{BD=ED}\end{array}\right.$,
∴△ADB≌△CDE(SAS),
∴∠BAD=∠ACB=40°,
∴∠BAC=40°+40°=80°;
(2)如图2,过B作BN∥AC,交HF的延长线于N,直线HF交AB于M,连接DH、DM,
∴∠BNM=∠EHF,
∵BF=EF,∠BFN=∠EFH,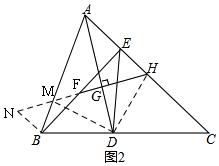
∴△EFH≌△BFN(AAS),
∴BN=EH,
由(1)得:∠BAD=∠DAC,
∵FH⊥AD,
∴∠AGF=∠AGH=90°,
∵AG=AG,
∴△AMG≌△AHG(ASA),
∴AH=AM,∠AHM=∠AMH,
∵∠AMH=∠BMN,
∴∠BNM=∠BMN,
∴BN=BM,
∵△ABD≌△CED,
∴∠ABD=∠CED,
∵BD=DE,
∴△DEH≌△DBM,
∴∠BMD=∠AHD,
∵AM=AH,
∠BAD=∠DAH,AD=AD,
∴△AMD≌△AHD,
∴∠AMD=∠AHD,
∴∠AMD=∠BMD,
∵∠AMD+∠BMD=180°,
∴∠AMD=90°,
∴∠AHD=90°,
∵AD=CD,
∴AH=CH.
点评 本题考查了三角形全等的性质和判定、等腰三角形三线合一的性质、平行线的性质、三角形的外角定理,作辅助线,构建三角形全等是关键,第二问比较复杂,熟练掌握三角形全等的判定是关键.


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
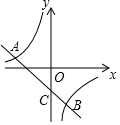 如图:一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(-3,1)、B(1,n)两点.
如图:一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A(-3,1)、B(1,n)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com