
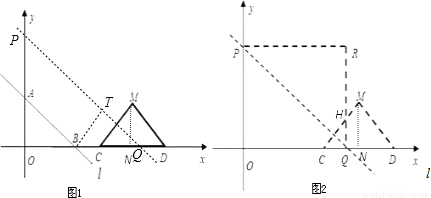
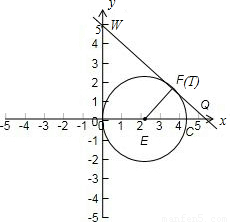
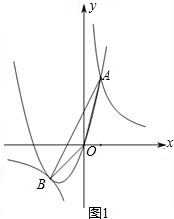
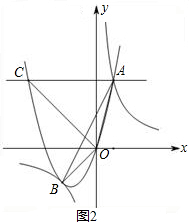
 x+3分别交x轴、y轴于B、A两点,等腰直角△CDM斜边落在x轴上,且CD=6,如图1所示.若直线l以每秒3个单位向上作匀速平移运动,同时点C从(6,0)开始以每秒2个单位的速度向右作匀速平移运动,如图2所示,设移动后直线l运动后分别交x轴、y轴于Q、P两点,以OP、OQ为边作如图矩形OPRQ.设运动时间为t秒.
x+3分别交x轴、y轴于B、A两点,等腰直角△CDM斜边落在x轴上,且CD=6,如图1所示.若直线l以每秒3个单位向上作匀速平移运动,同时点C从(6,0)开始以每秒2个单位的速度向右作匀速平移运动,如图2所示,设移动后直线l运动后分别交x轴、y轴于Q、P两点,以OP、OQ为边作如图矩形OPRQ.设运动时间为t秒.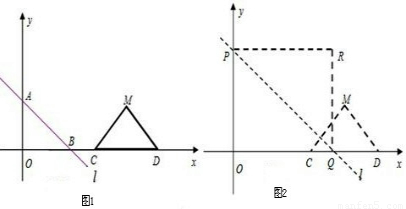
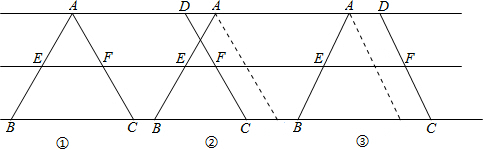
 CQ•QH,把CQ、QH代入即可求出答案;③当2.5<t<4时,如图(3)同法可求DQ,根据s=S△CMD-S△DQE,求出△CMD和△DQE的面积代入即可;④当t≥4时,s=S△CMD=
CQ•QH,把CQ、QH代入即可求出答案;③当2.5<t<4时,如图(3)同法可求DQ,根据s=S△CMD-S△DQE,求出△CMD和△DQE的面积代入即可;④当t≥4时,s=S△CMD= ×6×3=9;
×6×3=9;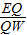 =
=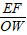 ,代入即可求出t的值,进一步得出t的取值范围.
,代入即可求出t的值,进一步得出t的取值范围.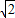 ,
,
 x+3,
x+3, x+3+3t,
x+3+3t, x+3+3t,
x+3+3t,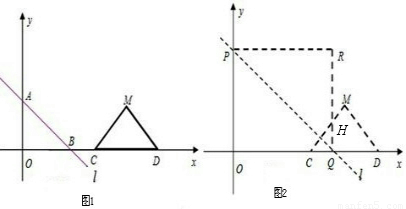
 CQ•QH=
CQ•QH= (2t-2)2=2t2-4t+2,
(2t-2)2=2t2-4t+2,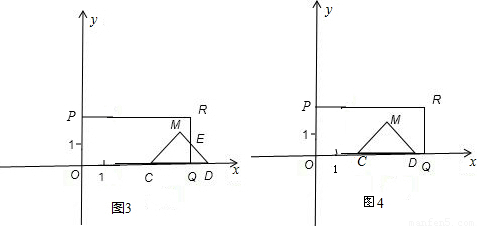
 ×6×3-
×6×3- (8-2t)2=-2t2+16t-23,
(8-2t)2=-2t2+16t-23, ×6×3=9;
×6×3=9;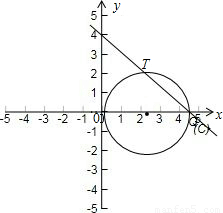
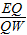 =
= ,
,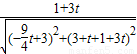 =
=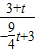 ,
,

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
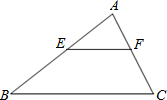 如图,在△ABC中,AE=EB,AF=FC,有一同学发现EF与BC存在以下关系:EF∥BC,且EF=
如图,在△ABC中,AE=EB,AF=FC,有一同学发现EF与BC存在以下关系:EF∥BC,且EF=| 1 | 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
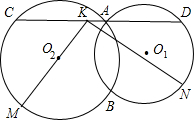 如图,⊙O1与⊙O2相交于点A和B,经过A作直线与⊙O1相交于D,与⊙O2相交于C,设弧BC的中点为M,弧BD的中点为N,线段CD的中点为K.求证:MK⊥KN.
如图,⊙O1与⊙O2相交于点A和B,经过A作直线与⊙O1相交于D,与⊙O2相交于C,设弧BC的中点为M,弧BD的中点为N,线段CD的中点为K.求证:MK⊥KN.查看答案和解析>>
科目:初中数学 来源: 题型:
| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
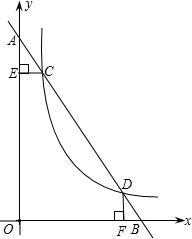 函数y=
函数y=| m | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 25、已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
25、已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com