
【题目】某公司招聘一名职员,先对应聘者进行笔试考核,笔试进入前两名的选手再进入面试方面的考核,最终在参加面试的两人中录取一人.该公司将应聘者的笔试成绩划分了4个等级:设应聘者的成绩为x(单位:分),当60≤x<70时为不合格;当70≤x<80时为合格;当80≤x<90时为良好;当90≤x≤100时为优秀.下面是参加笔试的10名应聘者的成绩:86 75 67 86 92 75 82 90 86 78
(1)这10名应聘者的笔试成绩的中位数是_______,众数是_______;
(2)请将下面表示上述4个等级的统计图补充完整;
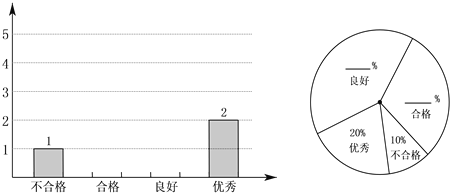
(3)该公司对进入笔试前两名的甲、乙二人进行了面试考核,面试中包括形体、口才、人际交往、创新能力,他们的成绩(百分制)如下表:
候选人 | 面试项目 | |||
形体 | 口才 | 人际交往 | 创新能力 | |
甲 | 86 | 90 | 95 | 90 |
乙 | 95 | 85 | 90 | 92 |
如果公司根据经营性质和岗位要求,以面试成绩中形体占10%,口才占20%,人际交往40%,创新能力占30%确定成绩,那么你认为该公司应该录取谁?请通过计算说明理由.
【答案】(1)84;86;(2)见解析;(3)录取甲,理由见解析.
【解析】
(1)把这组数据从小到大排列,根据中位数和众数的定义即可得答案;
(2)根据成绩得出个等级人数,进而求出合格和良好的百分比,据此补全统计图即可;
(3)分别计算甲、乙两人的平均成绩,即可得答案.
(1)把这组数据从小到大排列得:67 75 75 78 82 86 86 86 90 92,
∵中间两个数据为82和86,
∴这组数据的中位数是![]() =84,
=84,
∵这组数据86出现的次数最多,
∴这组数据的众数是86,
故答案为:84;86
(2)∵合格的有:75、75、78,共3人,良好的有:82、86、86、86,共4人,
∴合格的百分比为![]() ×100%=30%,良好的百分比为
×100%=30%,良好的百分比为![]() ×100%=40%,
×100%=40%,
∴补全统计图如下:
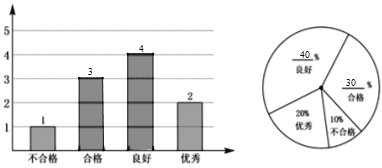
(3)甲的平均成绩为:86×10%+90×20%+95×40%+90×30%=91.6.
乙的平均成绩为:95×10%+85×20%+90×40%+92×30%=90.1.
∵91.6>90.1,
∴应该录取甲.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在扇形![]() 中,
中,![]() ,半径
,半径![]() ,点P为
,点P为![]() 上任一点(不与A、O重合).
上任一点(不与A、O重合).
(1)如图①,Q是![]() 上一点,若
上一点,若![]() ,求证:
,求证:![]() .
.
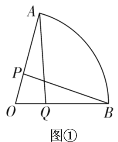
(2)如图②,将扇形沿![]() 折叠,得到O的对称点
折叠,得到O的对称点![]() .
.
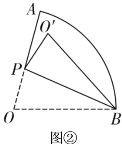
①若点![]() 落在
落在![]() 上,求
上,求![]() 的长;
的长;
②当![]() 与扇形
与扇形![]() 所在的圆相切时,求折痕的长.(注:本题结果不取近似值)
所在的圆相切时,求折痕的长.(注:本题结果不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
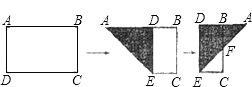
【题目】如图,有一块矩形纸片ABCD,AB=8,AD=6.将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位现要组织其市场和生产部的员工游览该公园,门票价格如下:
购票人数 | 1~50 | 51~100 | 100以上 |
门票价格 | 13元/人 | 11元/人 | 9元/人 |
如果按部门作为团体,选择两个不同的时间分别购票游览公园,则共需支付门票费为1245元;如果两个部门合在一起作为一个团体,同一时间购票游览公园,则需支付门票费为945元.那么该公司这两个部的人数之差的绝对值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,过点C作⊙O的切线,交直径AB的延长于点D,若∠ABC=65°,则∠D的度数是( )

A.25°B.30°C.40°D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑤5a﹣2b<0;其中正确的个数有( )
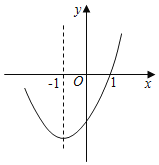
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
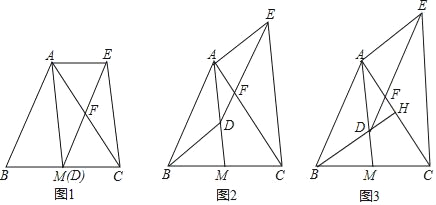
【题目】如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE∥AB交AC于点F,CE∥AM,连结AE.
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM.
①求∠CAM的度数;
②当FH=![]() ,DM=4时,求DH的长.
,DM=4时,求DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,弦AB垂直平分半径OC,垂足为D.若点P是⊙O上异于点A,B的任意一点,则∠APB=( )
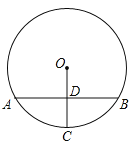
A.30°或60°B.60°或150°C.30°或150°D.60°或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
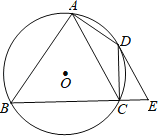
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,点E在BC的延长线上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AC∥DE,当AB=8,CE=2时,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com