
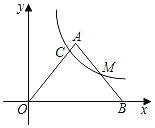
【题目】如图,在平面直角坐标系中,△OAB的边OB在x轴的正半轴上,AO=AB,M是边AB的中点,经过点M的反比例函数y=![]() (k>0,x>0)的图象与边OA交于点C,则
(k>0,x>0)的图象与边OA交于点C,则![]() 的值为__.
的值为__.
【答案】![]()
【解析】
过点C、点A、点M作x轴的垂线CD、AE、MF,由平行线截线段成比例定理可得![]() =
=![]() =
=![]() ;再由三角形的中位线定理得出MF=
;再由三角形的中位线定理得出MF=![]() AE,EF=BF=
AE,EF=BF=![]() BE=
BE=![]() OE,从而OF=
OE,从而OF=![]() OE;由点C和点M均在反比例函数y=
OE;由点C和点M均在反比例函数y=![]() (k>0,x>0)的图象上,得出ODCD=OFMF=k,将前面所得的相关线段的数量关系代入化简,得出
(k>0,x>0)的图象上,得出ODCD=OFMF=k,将前面所得的相关线段的数量关系代入化简,得出![]() ·
·![]() =
=![]() ,则可求得答案.
,则可求得答案.
解:如图,过点C、点A、点M作x轴的垂线CD、AE、MF,
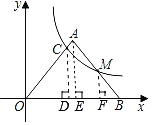
则CD∥AE∥MF,
∴![]() =
=![]() =
=![]() ,
,
∵AO=AB,AE⊥x轴,
∴OE=BE,
∵M是边AB的中点,MF∥AE,
∴MF=![]() AE,EF=BF=
AE,EF=BF=![]() BE=
BE=![]() OE,
OE,
∴OF=![]() OE,
OE,
∵点C和点M均在反比例函数y=![]() (k>0,x>0)的图象上,
(k>0,x>0)的图象上,
∴ODCD=OFMF=k,
∴ODCD=![]() OE×
OE×![]() AE,
AE,
∴![]() =
=![]() ,
,
∵![]() =
=![]() =
=![]() ,
,
∴![]() ·
·![]() =
=![]() ,
,
∴![]() =
=![]() ,(负值舍去).
,(负值舍去).
故答案为:![]() .
.


 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
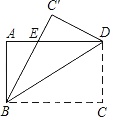
【题目】如图将一张矩形纸片ABCD沿对角线BD翻折,点C的对应点为C′,AD与BC′交于点E,若∠ABE=30°,BC=3,则DE的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宜跟几位同学在某快餐厅吃饭,如图为此快餐厅的菜单.若他们所点的餐食总共为10份盖饭,x杯饮料,y份凉拌菜.
(1)他们点了 份A套餐, 份B套餐, 份C套餐(均用含x或y的代数式表示);
(2)若x=6,且A、B、C套餐均至少点了1份,则最多有 种点餐方案.

查看答案和解析>>
科目:初中数学 来源: 题型:
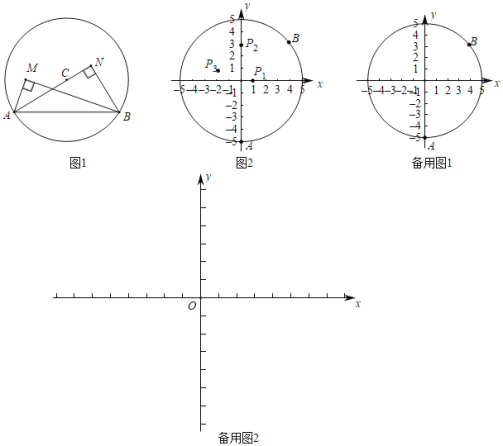
【题目】A,B是⊙C上的两个点,点P在⊙C的内部.若∠APB为直角,则称∠APB为AB关于⊙C的内直角,特别地,当圆心C在∠APB边(含顶点)上时,称∠APB为AB关于⊙C的最佳内直角.如图1,∠AMB是AB关于⊙C的内直角,∠ANB是AB关于⊙C的最佳内直角.在平面直角坐标系xOy中.
(1)如图2,⊙O的半径为5,A(0,﹣5),B(4,3)是⊙O上两点.
①已知P1(1,0),P2(0,3),P3(﹣2,1),在∠AP1B,∠AP2B,∠AP3B,中,是AB关于⊙O的内直角的是 ;
②若在直线y=2x+b上存在一点P,使得∠APB是AB关于⊙O的内直角,求b的取值范围.
(2)点E是以T(t,0)为圆心,4为半径的圆上一个动点,⊙T与x轴交于点D(点D在点T的右边).现有点M(1,0),N(0,n),对于线段MN上每一点H,都存在点T,使∠DHE是DE关于⊙T的最佳内直角,请直接写出n的最大值,以及n取得最大值时t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是由五个完全相同的小正方体组成的立体图形.将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是( )

A.主视图B.俯视图
C.左视图D.主视图、俯视图和左视图都改变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面内有一点![]() 到
到![]() 的三个顶点的距离分别为
的三个顶点的距离分别为![]() 若有
若有![]() ,则称点
,则称点![]() 为
为![]() 关于点
关于点![]() 的勾股点.
的勾股点.
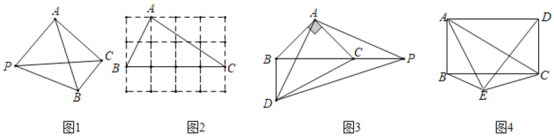
![]() 如图2,在
如图2,在![]() 的方格纸中,每个小正方形的边长均为
的方格纸中,每个小正方形的边长均为![]() 的顶点在格点上,请找出所有的格点
的顶点在格点上,请找出所有的格点![]() ,使点
,使点![]() 为
为![]() 关于点
关于点![]() 的勾股点;
的勾股点;
![]() 如图3,
如图3, ![]() 为等腰直角三角形,
为等腰直角三角形,![]() 是斜边
是斜边![]() 延长线上一点,连接
延长线上一点,连接![]() ,以
,以![]() 为直角边作等腰直角三角形
为直角边作等腰直角三角形 ![]() (点
(点![]() 顺时针排列),
顺时针排列),![]() ,连接
,连接 ![]() 求证:点
求证:点![]() 为
为![]() 关于点
关于点![]() 的勾股点;
的勾股点;
![]() 如图4,点
如图4,点![]() 是矩形
是矩形![]() 外一点,且点
外一点,且点![]() 是
是![]() 关于点
关于点![]() 的勾股点,若
的勾股点,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
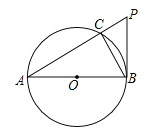
【题目】如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PCPA;
(3)当AC=6,CP=3时,求sin∠PAB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
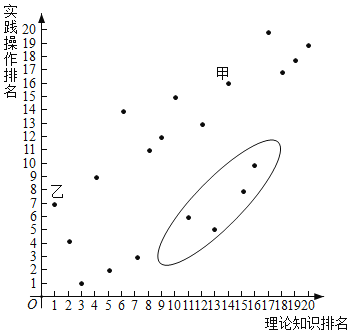
【题目】某公司计划招募10名技术人员,他们对20名面试合格人员进行了测试,测试包括理论知识和实践操作两部分,20名应聘者的成绩排名情况如图所示,下面有3个推断:
①甲测试成绩非常优秀,入选的可能性很大;
②乙的理论知识排名比实践操作排名靠前;
③位于椭圆形区域内的应聘者应该加强该专业理论知识的学习;
其中合理的是_____.(写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
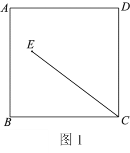
【题目】四边形![]() 是正方形,将线段
是正方形,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() .
.
(1)依题意补全图1;
(2)直接写出![]() 的度数;
的度数;
(3)连接![]() ,用等式表示线段
,用等式表示线段![]() 与
与![]() 的数量关系,并证明.
的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com