
分析 (1)求出OD的长,根据时间=$\frac{路程}{速度}$,计算即可.
(2)要使△PQB为直角三角形,显然只有∠PQB=90°或∠PBQ=90°,分两种情形分别列出方程,即可解决问题.
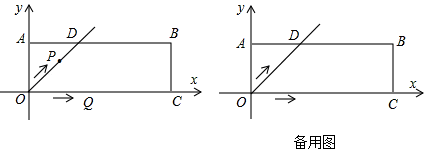
解答 解:(1)∵四边形OABC是矩形,
∴∠AOC=∠OAB=90°,
∵OD平分∠AOC,
∴∠AOD=∠DOQ=45°,
∴AO=OD=2,DO=2$\sqrt{2}$,
∴t=$\frac{2\sqrt{2}}{\sqrt{2}}$=2.
(2)要使△PQB为直角三角形,显然只有∠PQB=90°或∠PBQ=90°,
如图1,作PG⊥OC于点G,在Rt△POG中,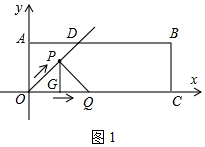
∵∠POQ=45°,
∴∠OPG=45°,
∵OP=$\sqrt{2}$t,
∴OG=PG=t,
∴点P的坐标为(t,t),
又∵Q(2t,0),B(6,2),
根据勾股定理:PB2=(6-t)2+(2-t)2,QB2=(6-2t)2+22,PQ2=(2t-t)2+t2=2t2,
①若∠PQB=90°,则有PB2=PQ2+BQ2,
即:(6-t)2+(2-t)2=(6-2t)2+2t,
解得:t=2或0(舍去),
∴t=2.
②若∠PBQ=90°,则有PQ2=PB2+BQ2,
∴(6-t)2+(2-t)2+(6-2t)2=2t2,
解得:t=5±$\sqrt{5}$.
∴t=2或5±$\sqrt{5}$时,△pqb为直角三角形.
点评 本题考查矩形的性质、坐标与图形性质、两点间距离公式、勾股定理等知识,解题的关键是学会用分类讨论的思想思考问题,学会构建方程解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com