
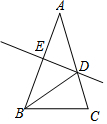
 如图,△ABC中,AB的垂直平分线交AC于D,已知AC=10cm,BC=7cm,则△BCD的周长是17cm.
如图,△ABC中,AB的垂直平分线交AC于D,已知AC=10cm,BC=7cm,则△BCD的周长是17cm. 科目:初中数学 来源: 题型:选择题
| A. | 随机抛掷一枚硬币,反面一定朝上 | |
| B. | 数据3,3,5,5,8的众数是8 | |
| C. | 某商场抽奖活动获奖的概率为$\frac{1}{50}$,说明毎买50张奖券中一定有一张中奖 | |
| D. | 想要了解广安市民对“全面二孩”政策的看法,宜采用抽样调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 若m,n为正实数,t是关于x的方程x2+2mx=n2的一正实数根,
若m,n为正实数,t是关于x的方程x2+2mx=n2的一正实数根,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,梯形ABCD中,AD∥BC,AD:BC=1:3,对角线AC与BD相交于点O,AE⊥BC,垂足为E,AE恰好过BD的中点F,∠FBE=30°
如图,梯形ABCD中,AD∥BC,AD:BC=1:3,对角线AC与BD相交于点O,AE⊥BC,垂足为E,AE恰好过BD的中点F,∠FBE=30°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com