
����Ŀ����ƽ��ֱ������ϵ�У�������y=�� ![]() x2+bx+c��x�ύ�ڵ�A��B����y�ύ�ڵ�C��ֱ��y=x+4����A��C���㣮
x2+bx+c��x�ύ�ڵ�A��B����y�ύ�ڵ�C��ֱ��y=x+4����A��C���㣮
��1���������ߵĽ���ʽ��
��2����AC�Ϸ�������������һ����P��
����ͼ1������P�˶���ijλ��ʱ����AP��AOΪ�ڱߵ�ƽ���ı��ε��ĸ�����ǡ��Ҳ���������ϣ������ʱ��P�����ꣻ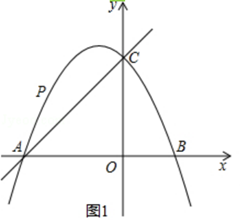
����ͼ2������O��P��ֱ��y=kx��AC�ڵ�E����PE��OE=3��8����k��ֵ��
���𰸡�
��1��
�⣺��ֱ��y=x+4����A��C���㣬
��A�������ǣ���4��0������C�����ǣ�0��4����
�֡������߹�A��C���㣬
��  ����ã�
����ã� ![]() ��
��
�������ߵĽ���ʽΪ ![]() ��
��
��2��
�⣺����ͼ1
�� ![]() ��
��
�������ߵĶԳ�����ֱ��x=��1��
����AP��AOΪ�ڱߵ�ƽ���ı��εĵ��ĸ�����Qǡ��Ҳ���������ϣ�
��PQ��AO��PQ=AO=4��
��P��Q�����������ϣ�
��P��Q����ֱ��x=��1�Գƣ�
��P��ĺ������ǩ�3��
�൱x=��3ʱ�� ![]() ��
��
��P��������� ![]() ��
��
�ڹ�P����PF��OC��AC�ڵ�F��
��PF��OC��
���PEF�ס�OEC��
�� ![]() ��
��
�֡� ![]() ��
��
�� ![]() ��
��
���F��x��x+4��
�� ![]() ��
��
����ã�x2+4x+3=0����ã�x1=��1��x2=��3��
��x=��1ʱ�� ![]() ����x=��3ʱ��
����x=��3ʱ�� ![]() ��
��
��P�������� ![]() ��
�� ![]() ��
��
�֡ߵ�P��ֱ��y=kx�ϣ�
�� ![]() ��
��

����������1����ֱ�ߵĽ���ʽy=x+4�����A�͵�C�����꣬��A��C������ֱ����y=�� ![]() x2+bx+c���b��c��ֵ���ɵõ������ߵĽ���ʽ����2��������AP��AOΪ�ڱߵ�ƽ���ı��εĵ��ĸ�����Qǡ��Ҳ���������ϣ���PQ��AO���ٸ��������ߵĶԳ���������P�ĺ����꣬�ɣ�1���е������߽���ʽ������������������꣬����ý⣻
x2+bx+c���b��c��ֵ���ɵõ������ߵĽ���ʽ����2��������AP��AOΪ�ڱߵ�ƽ���ı��εĵ��ĸ�����Qǡ��Ҳ���������ϣ���PQ��AO���ٸ��������ߵĶԳ���������P�ĺ����꣬�ɣ�1���е������߽���ʽ������������������꣬����ý⣻
�ڹ�P����PF��OC��AC�ڵ�F����ΪPF��OC�����ԡ�PEF�ס�OEC�������������ε����ʣ���Ӧ�ߵı�ֵ��ȿ����PF�ij�������������F��x��x+4�������� ![]() �������x��ֵ���ⷽ�����x��ֵ�ɵõ�P�����꣬����ֱ��y=kx�������k��ֵ��
�������x��ֵ���ⷽ�����x��ֵ�ɵõ�P�����꣬����ֱ��y=kx�������k��ֵ��
�����㾫����������Ŀ����֪���������ö��κ��������ʺ����������ε��ж������ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С�����������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��bΪʵ������b= ![]() ��
��
��1���� ![]() ��ֵ��
��ֵ��
��2���� ![]() ��ֵ�ǹ���x��һԪ���η���x2��2x+k2+k=0��һ��������k����һ������
��ֵ�ǹ���x��һԪ���η���x2��2x+k2+k=0��һ��������k����һ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AC=12cm��BD=16cm������N�ӵ�D���������߶�DB��2cm/s���ٶ����B�˶���ͬʱ����M�ӵ�B���������߶�BA��1cm/s���ٶ����A�˶���������һ������ֹͣ�˶�ʱ��һ������Ҳ��ֹ֮ͣ�����˶�ʱ��Ϊt��s����t��0�����Ե�MΪԲ�ģ�MB��Ϊ�뾶�ġ�M������BA���߶�BD�ֱ��ڵ�E��F������EN�� 
��1����BF�ij����ú���t�Ĵ���ʽ��ʾ���������t��ȡֵ��Χ��
��2����tΪ��ֵʱ���߶�EN���M���У�
��3������M���߶�ENֻ��һ�������㣬��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У��뾶��Ϊ1����λ���ȵİ�ԲO1��O2��O3 �� �����һ��ƽ�������ߣ���P��ԭ��O���������������������˶����ٶ�Ϊÿ�� ![]() ����λ���ȣ����2017��ʱ����P�������ǣ� ��
����λ���ȣ����2017��ʱ����P�������ǣ� ��
A.��2016��0��
B.��2017��1��
C.��2017����1��
D.��2018��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����y= ![]() ��x��0����ͼ����A��B����B������Ϊ��2��2��������A��AC��x�ᣬ����ΪC������B��BD��y�ᣬ����ΪD��AC��BD���ڵ�F��һ�κ���y=ax+b��ͼ����A��D����x��ĸ����ύ�ڵ�E
��x��0����ͼ����A��B����B������Ϊ��2��2��������A��AC��x�ᣬ����ΪC������B��BD��y�ᣬ����ΪD��AC��BD���ڵ�F��һ�κ���y=ax+b��ͼ����A��D����x��ĸ����ύ�ڵ�E 
��1����AC= ![]() OD����a��b��ֵ��
OD����a��b��ֵ��
��2����BC��AE����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��3x+k=0������ʵ����x1��x2
��1����ʵ��k��ȡֵ��Χ��
��2����|x1��x2|=3��x1x2ʱ����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC=10��BC=12������P��A���������A��B�ķ�����AB���ƶ�������Q��B���������B��C�ķ�����BC���ƶ�����P�㵽���Bʱ��P���Q��ֹͣ�ƶ�����������ƶ��ٶ���ȣ�����PA=x����BPQ�����Ϊy����y����x�ĺ���ͼ������ǣ� ��
A.
B.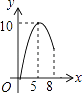
C.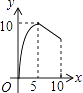
D.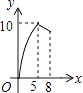
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC�ڽ��ڡ�O��D�� ![]() ��һ�㣬OD��BC������ΪH��
��һ�㣬OD��BC������ΪH��
��1����ͼ1����Բ��O��AB����ʱ����֤��AC=2OH�� 
��2����ͼ2����Բ��O�ڡ�ABC�ⲿʱ������AD��CD��AD��BC���ڵ�P����֤����ACD=��APB�� 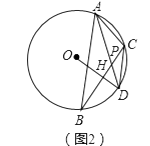
��3���ڣ�2���������£���ͼ3������BD��EΪ��O��һ�㣬����DE��BC�ڵ�Q����AB�ڵ�N������OE��BFΪ��O���ң�BF��OE�ڵ�R��DE�ڵ�G������ACD����ABD=2��BDN��AC=5 ![]() ��BN=3
��BN=3 ![]() ��tan��ABC=
��tan��ABC= ![]() ����BF�ij���
����BF�ij��� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У��Ե�AΪԲ�ģ�AB��Ϊ�뾶������AD�ڵ�F���ٷֱ��Ե�B��FΪԲ�ģ����� ![]() BF��Ϊ�뾶��������������һ��P����
BF��Ϊ�뾶��������������һ��P����
��AP���ӳ���BC�ڵ�E������EF��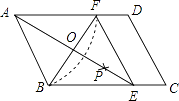
��1���ı���ABEF������ѡ����Ρ����Ρ������Ρ���ȷ������ֱ����д�����
��2��AE��BF�ཻ�ڵ�O�����ı���ABEF���ܳ�Ϊ40��BF=10����AE�ij�Ϊ �� ��ABC=�㣮��ֱ����д�����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com