
在下列条件中:①∠A+∠B=∠C;②∠A:∠B∠:∠C=1:2:3;③∠A=90°-∠B;④∠A=∠B=∠C,能确定△ABC是直角三角形的条件有( )个.
A.1 B.2 C.3 D.4
科目:初中数学 来源: 题型:
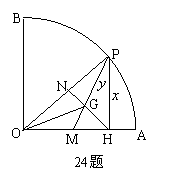
如图, 在半径为6,圆心角为90°的扇形OAB的弧AB上, 有一个动点P, PH⊥OA,垂足为H, △PHO的中线PM与NH交于点G.
有一个动点P, PH⊥OA,垂足为H, △PHO的中线PM与NH交于点G.
(1)求证: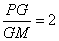 ;
;
(2)设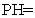
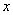 ,
, 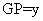 ,求
,求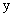 关于
关于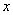 的函数解析式,并写自变量
的函数解析式,并写自变量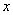 的取值范围;
的取值范围;
(3)如果△PGH是等腰三角形,试求出线段PH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
某公司有 型产品40件,
型产品40件, 型产品60件,分配给下属甲、乙两
型产品60件,分配给下属甲、乙两 个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
|
|
| |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
(1)设分配给甲店 型产品
型产品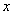 件,这家公司卖出这100件产品的总利润为
件,这家公司卖出这100件产品的总利润为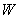 (元),求
(元),求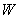 关于
关于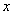 的函数关系式,并求出
的函数关系式,并求出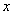 的取值范围;
的取值范围;
(2)若公司要求总利润不低于17560元,说明有多少种不同分配 方案,并将
方案,并将 各种方案设计出来;
各种方案设计出来;
(3)为了促销,公司决定仅对甲店 型产品让利销售,每件让利
型产品让利销售,每件让利 元,但让利后
元,但让利后 型产品的每件利润仍高于甲店
型产品的每件利润仍高于甲店 型产品的每件利润.甲店的
型产品的每件利润.甲店的 型产品以及乙店的
型产品以及乙店的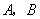 型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等,其中真命题的个数有( )
A、3个 B、2个 C、1个 D、0个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com