
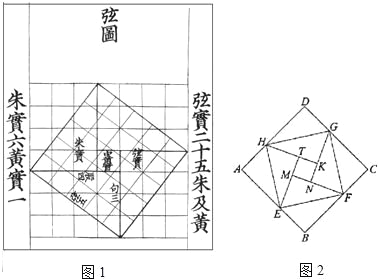
【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一副“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是由八个全等的直角三角形拼接而成.记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=10,则S2的值是_________.
科目:初中数学 来源: 题型:
【题目】如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为( )

A. 12秒 B. 16秒 C. 20秒 D. 30秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整;
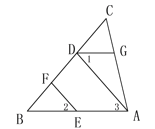
解:∵EF∥AD
∴ =∠3 (两直线平行,同位角相等)
又∵∠1=∠2
∴∠1=∠3 (__________________)
∴ ∥DG (__________________________)
∴∠BAC+______=180°(_________________________)
∵∠BAC=70°
∴∠AGD=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
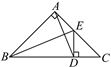
【题目】如图,△ABC是等腰直角三角形,∠BAC=90°,BE是△ABC的角平分线,ED⊥BC于点D,连接AD.
(1)请你写出图中所有的等腰三角形;
(2)若BC=10,求AB+AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列证明:如图,已知AD⊥BC,EF⊥BC,∠1=∠2.
求证: DG∥BA.
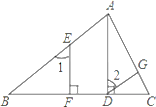
证明:∵AD⊥BC,EF⊥BC ( 已知 )
∴∠EFB=90°,∠ADB=90°(_______________________ )
∴∠EFB=∠ADB ( 等量代换 )
∴EF∥AD ( _________________________________ )
∴∠1=∠BAD (________________________________________)
又∵∠1=∠2 ( 已知)
∴ (等量代换)
∴DG∥BA. (__________________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与理解:
三角形中一边中点与这边所对顶点的线段称为三角形的中线。
三角形的中线的性质:三角形的中线等分三角形的面积。
即如图1,AD是![]() 中BC边上的中线,则
中BC边上的中线,则![]() ,
,
理由:![]() ,
,![]() ,
,
即:等底同高的三角形面积相等。
操作与探索:

在如图2至图4中,![]() 的面积为a。
的面积为a。
(1)如图2,延长![]() 的边BC到点D,使CD=BC,连接DA,若
的边BC到点D,使CD=BC,连接DA,若![]() 的面积为
的面积为![]() ,则
,则![]() (用含a的代数式表示);
(用含a的代数式表示);
(2)如图3,延长![]() 的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,若
的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE,若![]() 的面积为
的面积为![]() ,则
,则![]() _________(用含a的代数式表示);
_________(用含a的代数式表示);
(3)在图3的基础上延长AB到点F,使BF=AB,连接FD,FE,得到![]() (如图4),若阴影部分的面积为
(如图4),若阴影部分的面积为![]() ,则
,则![]() ________(用含a的代数式表示)
________(用含a的代数式表示)
(4)拓展与应用:
如图5,已知四边形ABCD的面积是a;E,F,G,H分别是AB,BC,CD的中点,求图中阴影部分的面积?

查看答案和解析>>
科目:初中数学 来源: 题型:
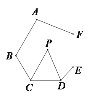
【题目】如图,在六边形ABCDEF中,∠A+∠B+∠E+∠F=α,CP、DP分别平分∠BCD、∠CDE,则∠P的度数是( )
A. ![]() α-180°B. 180°-
α-180°B. 180°-![]() C.
C. ![]() D. 360°-
D. 360°-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
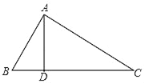
【题目】题目:如图,在△ABC中,点D是BC边上一点,连结AD,若AB=10,AC=17,BD=6,AD=8,解答下列问题:
(1)求∠ADB的度数;
(2)求BC的长.
小强做第(1)题的步骤如下:∵AB2=BD2+AD2
∴△ABD是直角三角形,∠ADB=90°.
(1)小强解答第(1)题的过程是否完整,如果不完整,请写出第(1)题完整的解答过程
(2)完成第(2)题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
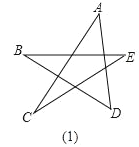
(1)请你根据已经学过的知识求出下面星形图(1)中∠A+∠B+∠C+∠D+∠E的度数;
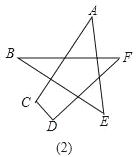
(2)若对图(1)中星形截去一个角,如图(2),请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数;
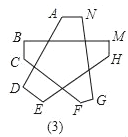
(3)若再对图(2)中的角进一步截去,你能由题(2)中所得的方法或规律,猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗?只要写出结论,不需要写出解题过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com