
【题目】△ABC为等腰直角三角形,∠ACB=90°,AC=BC=2,P为线段AB上一动点,D为BC上中点,则PC+PD的最小值为( )
A.![]() B.3 C.
B.3 C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
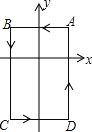
【题目】如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2015个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A—B—C-D—A一B一…的规律紧绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
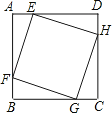
【题目】如图,已知:正方形EFGH的顶点E、F、G、H分别在正方形ABCD的边DA、AB、BC、CD上.若正方形ABCD的面积为16,AE=1,则正方形EFGH的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为___________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com