
【题目】阅读下题和解题过程:化简![]() ,使结果不含绝对值.
,使结果不含绝对值.
解:当![]() 时,即
时,即![]() 时,
时,
原式![]()
![]() ;
;
当![]() ,即
,即![]() 时,
时,
原式![]()
![]()
这种解题的方法叫“分类讨论法”.
(1)请你用“分类讨论法”解一元一次方程:![]() ;
;
(2)试探究:当![]() 分别为何值时,方程
分别为何值时,方程![]()
①无解,②只有一个解,③有两个解
科目:初中数学 来源: 题型:
【题目】某单位为响应政府发出的全民健身的号召,打算在长和宽分别为20 m和11 m的矩形大厅内修建一个60 m2的矩形健身房ABCD.该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图),已知装修旧墙壁的费用为20元/m2,新建(含装修)墙壁的费用为80元/m2.设健身房的高为3 m,一面旧墙壁AB的长为x m,修建健身房墙壁的总投入为y元.
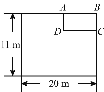
(1)求y与x的函数关系式;
(2)为了合理利用大厅,要求自变量x必须满足条件:8≤x≤12,当投入的资金为4800元时,问利用旧墙壁的总长度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年拟继续举办丽水市中学生汉字听写、诗词诵写大赛.经过初赛、复赛,选出了两个代表队参加市内7月份的决赛.两个队各选出的![]() 名选手的复赛成绩如图所示.
名选手的复赛成绩如图所示.
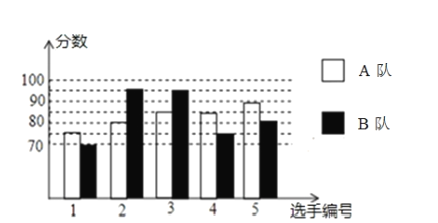
(1)根据图示补全下表;
平均数(分) | 中位数(分) | 众数(分) | |
|
|
| |
|
|
(2)结合两队成绩的平均数和中位数,分析哪个队的复赛成绩较好;
(3)计算两队成绩的方差,并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面;
B方法:剪4个侧面和5个底面.

现有38张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用x的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,则能做多少个盒子?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”,在Rt△ABC中,∠C=90°,若Rt△ABC是“好玩三角形”,则tanA= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,将
的中点,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后,点
后,点![]() 落在
落在![]() 的延长线上点
的延长线上点![]() 处,点
处,点![]() 落在点
落在点![]() 处.再将线段
处.再将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得线段
得线段![]() ,连接
,连接![]() ,
,![]() .
.
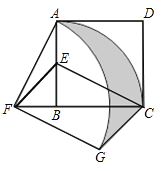
(1)求证:![]() ;
;
(2)求点![]() ,点
,点![]() 在旋转过程中形成的
在旋转过程中形成的![]() ,
,![]() 与线段
与线段![]() 所围成的阴影部分的面积.
所围成的阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在△ABC中,AD、BD分别平分∠BAC和∠ABC,AD、BD相交于点D,过点D作DE∥AC,DF∥BC分别交AB于点E、F.
①若∠EDF=80°,则∠ADB=________°;
②若∠C=![]() 则∠ADB=________°.
则∠ADB=________°.
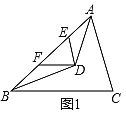
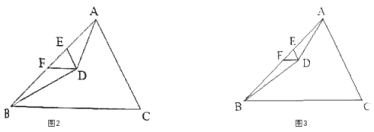
(2)如图2,在△ABC中,若∠BAD=![]() ∠BAC,∠ABD=
∠BAC,∠ABD=![]() ∠ABC,AD、BD相交于点D,过点D作DE∥AC,DF∥BC分别交AB于点E、F,若∠EDF=60°,则∠ADB=_______°;
∠ABC,AD、BD相交于点D,过点D作DE∥AC,DF∥BC分别交AB于点E、F,若∠EDF=60°,则∠ADB=_______°;
(3)如图3,在△ABC中,AD、BD分别是∠BAC、∠ABC的![]() 等分线,AD、BD相交于点D,若∠BAD=
等分线,AD、BD相交于点D,若∠BAD=![]() ∠BAC,∠ABD=
∠BAC,∠ABD=![]() ∠ABC,过点D作DE∥AC,DF∥BC分别交AB于点E、F,若∠EDF=
∠ABC,过点D作DE∥AC,DF∥BC分别交AB于点E、F,若∠EDF=![]() ,则∠ADB的度数是多少?(用
,则∠ADB的度数是多少?(用![]() 表示)
表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,射线
中,射线![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 边上运动(不与点
边上运动(不与点![]() 重合),过点
重合),过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
(1)如图1,点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 平分
平分![]() .
.


①若![]() ,
,![]() ,则
,则![]() _____;若
_____;若![]() ,则
,则![]() _____;
_____;
②试探究![]() 与
与![]() 之间的数量关系?请说明理由;
之间的数量关系?请说明理由;
(2)点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 的角平分线所在直线与射线
的角平分线所在直线与射线![]() 交于点
交于点![]() .试探究
.试探究![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com